Deep Learning for Outlier Detection on Tabular and Image Data
The challenges and promises of deep learning for outlier detection, including self-supervised learning techniquesIn the last several years, deep-learning approaches have proven to be extremely effective for many machine learning problems, and, not surprisingly, this has included several areas of outlier detection. In fact, for many modalities of data, including image, video, and audio, there’s really no viable option for outlier detection other than deep learning-based methods.At the same time, though, for tabular and time-series data, more traditional outlier detection methods can still very often be preferable. This is interesting, as deep learning tends to be a very powerful approach to so many problems (and deep learning has been able to solve many problems that are unsolvable using any other method), but tabular data particularly has proven stubbornly difficult to apply deep learning-based methods to, at least in a way that’s consistently competitive with more established outlier detection methods.In this article (and the next — the second focusses more on self-supervised learning for tabular data), I’ll take a look at why deep learning-based methods tend to work very well for outlier detection for some modalities (looking at image data specifically, but the same ideas apply to video, audio, and some other types of data), and why it can be limited for tabular data.As well, I’ll cover a couple reasons to nevertheless take a good look at deep learning for tabular outlier detection. One is that the area is moving quickly, holds a great deal of progress, and this is where we’re quite likely to see some of the largest advances in tabular outlier detection in the coming years.Another is that, while more traditional methods (including statistical tests such as those based on z-scores, interquartile ranges, histograms, and so on, as well as classic machine learning techniques such as Isolation Forests, k-Nearest Neighbors, Local Outlier Factor (LOF), and ECOD), tend to be preferable, there are some exceptions to this, and there are cases even today where deep-learning based approaches can be the best option for tabular outlier detection. We’ll take a look at these as well.This article continues a series on outlier detection, covering the use of subspaces, PCA, Distance Metric Learning, Shared Nearest Neighbors, Frequent Patterns Outlier Factor, Counts Outlier Detector, and doping.This article also contains an excerpt from my book, Outlier Detection in Python. That covers image data, and deep learning-based outlier detection, much more thoroughly, but this article provides a good introduction to the main ideas.Outlier Detection with Image DataAs indicated, with some data modalities, including image data, there are no viable options for outlier detection available today other than deep learning-based methods, so we’ll start by looking at deep learning-based outlier detection for image data.I’ll assume for this article, you’re reasonably familiar with neural networks and the idea of embeddings. If not, I’d recommend going through some of the many introductory articles online and getting up to speed with that. Unfortunately, I can’t provide that here, but once you have a decent understanding of neural networks and embeddings, you should be good to follow the rest of this.There are a number of such methods, but all involve deep neural networks in one way or another, and most work by generating embeddings to represent the images.Some of the most common deep learning-based techniques for outlier detection are based on autoencoders, variational autoencoders (VAEs), and Generative Adversarial Networks (GANs). I’ll cover several approaches to outlier detection in this article, but autoencoders, VAEs, and GANs are a good place to begin.These are older, well-established ideas and are examples of a common theme in outlier detection: tools or techniques are often developed for one purpose, and later found to be effective for outlier detection. Some of the many other examples include clustering, frequent item sets, Markov models, space-filling curves, and association rules.Given space constraints, I’ll just go over autoencoders in this article, but will try to cover VAEs, GANs, and some others in future articles. Autoencoders are a form of neural network actually designed originally for compressing data. (Some other compression algorithms are also used on occasion for outlier detection as well.)As with clustering, frequent item sets, association rules, Markov models, and so on, the idea is: we can use a model of some type to model the data, which then creates a concise summary of the main patterns in the data. For example, we can model the data by describing the clusters (if the data is well-clustered), the frequent item sets in the data, the linear relationships between the features, and so on. With autoencoders, we model the data with a compressed vector representation of the original data.These models will be able to repr

The challenges and promises of deep learning for outlier detection, including self-supervised learning techniques
In the last several years, deep-learning approaches have proven to be extremely effective for many machine learning problems, and, not surprisingly, this has included several areas of outlier detection. In fact, for many modalities of data, including image, video, and audio, there’s really no viable option for outlier detection other than deep learning-based methods.
At the same time, though, for tabular and time-series data, more traditional outlier detection methods can still very often be preferable. This is interesting, as deep learning tends to be a very powerful approach to so many problems (and deep learning has been able to solve many problems that are unsolvable using any other method), but tabular data particularly has proven stubbornly difficult to apply deep learning-based methods to, at least in a way that’s consistently competitive with more established outlier detection methods.
In this article (and the next — the second focusses more on self-supervised learning for tabular data), I’ll take a look at why deep learning-based methods tend to work very well for outlier detection for some modalities (looking at image data specifically, but the same ideas apply to video, audio, and some other types of data), and why it can be limited for tabular data.
As well, I’ll cover a couple reasons to nevertheless take a good look at deep learning for tabular outlier detection. One is that the area is moving quickly, holds a great deal of progress, and this is where we’re quite likely to see some of the largest advances in tabular outlier detection in the coming years.
Another is that, while more traditional methods (including statistical tests such as those based on z-scores, interquartile ranges, histograms, and so on, as well as classic machine learning techniques such as Isolation Forests, k-Nearest Neighbors, Local Outlier Factor (LOF), and ECOD), tend to be preferable, there are some exceptions to this, and there are cases even today where deep-learning based approaches can be the best option for tabular outlier detection. We’ll take a look at these as well.
This article continues a series on outlier detection, covering the use of subspaces, PCA, Distance Metric Learning, Shared Nearest Neighbors, Frequent Patterns Outlier Factor, Counts Outlier Detector, and doping.
This article also contains an excerpt from my book, Outlier Detection in Python. That covers image data, and deep learning-based outlier detection, much more thoroughly, but this article provides a good introduction to the main ideas.
Outlier Detection with Image Data
As indicated, with some data modalities, including image data, there are no viable options for outlier detection available today other than deep learning-based methods, so we’ll start by looking at deep learning-based outlier detection for image data.
I’ll assume for this article, you’re reasonably familiar with neural networks and the idea of embeddings. If not, I’d recommend going through some of the many introductory articles online and getting up to speed with that. Unfortunately, I can’t provide that here, but once you have a decent understanding of neural networks and embeddings, you should be good to follow the rest of this.
There are a number of such methods, but all involve deep neural networks in one way or another, and most work by generating embeddings to represent the images.
Some of the most common deep learning-based techniques for outlier detection are based on autoencoders, variational autoencoders (VAEs), and Generative Adversarial Networks (GANs). I’ll cover several approaches to outlier detection in this article, but autoencoders, VAEs, and GANs are a good place to begin.
These are older, well-established ideas and are examples of a common theme in outlier detection: tools or techniques are often developed for one purpose, and later found to be effective for outlier detection. Some of the many other examples include clustering, frequent item sets, Markov models, space-filling curves, and association rules.
Given space constraints, I’ll just go over autoencoders in this article, but will try to cover VAEs, GANs, and some others in future articles. Autoencoders are a form of neural network actually designed originally for compressing data. (Some other compression algorithms are also used on occasion for outlier detection as well.)
As with clustering, frequent item sets, association rules, Markov models, and so on, the idea is: we can use a model of some type to model the data, which then creates a concise summary of the main patterns in the data. For example, we can model the data by describing the clusters (if the data is well-clustered), the frequent item sets in the data, the linear relationships between the features, and so on. With autoencoders, we model the data with a compressed vector representation of the original data.
These models will be able to represent the typical items in the data usually quite well (assuming the models are well-constructed), but often fail to model the outliers well, and so can be used to help identify the outliers. For example, with clustering (i.e., when using a set of clusters to model the data), outliers are the records that don’t fit well into the clusters. With frequent item sets, outliers are the records that contain few frequent items sets. And with autoencoders, outliers are the records that do not compress well.
Where the models are forms of deep neural networks, they have the advantage of being able to represent virtually any type of data, including image. Consequently, autoencoders (and other deep neural networks such as VAEs and GANs) are very important for outlier detection with image data.
Many outlier detectors are also are built using a technique called self-supervised learning (SSL). These techniques are possibly less widely used for outlier detection than autoencoders, VAEs, and GANs, but are very interesting, and worth looking at, at least quickly, as well. I’ll cover these below, but first I’ll take a look at some of the motivations for outlier detection with image data.
Motivations for Outlier Detection with Image Data
One application is with self-driving cars. Cars will have multiple cameras, each detecting one or more objects. The system will then make predictions as to what each object appearing in the images is. One issue faced by these systems is that when an object is detected by a camera, and the system makes a prediction as to what type of object it is, it may predict incorrectly. And further, it may predict incorrectly, but with high confidence; neural networks can be particularly inclined to show high confidence in the best match, even when wrong, making it difficult to determine from the classifier itself if the system should be more cautious about the detected objects. This can happen most readily where the object seen is different from any of the training examples used to train the system.
To address this, outlier detection systems may be run in parallel with the image classification systems, and when used in this way, they’re often specifically looking for items that appear to be outside the distribution of the training data, referred to as out-of-distribution data, OOD.
That is, any vision classification system is trained on some, probably very large, but finite, set of objects. With self-driving cars this may include traffic lights, stop signs, other cars, buses, motorcycles, pedestrians, dogs, fire hydrants, and so on (the model will be trained to recognize each of these classes, being trained on many instances of each). But, no matter how many types of items the system is trained to recognize, there may be other types of (out-of-distribution) object that are encountered when on the roads, and it’s important to determine when the system has encountered an unrecognized object.
This is actually a common theme with outlier detection with image data: we’re very often interested in identifying unusual objects, as opposed to unusual images. That is, things like unusual lighting, colouring, camera angles, blurring, and other properties of the image itself are typically less interesting. Often the background as well, can be distracting from the main goal of identifying unusual items. There are exceptions to this, but this is fairly common, where we are interested really in the nature of the primary object (or a small number of relevant objects) shown in a picture.
Misclassifying objects with self-driving cars can be quite a serious problem — the vehicle may conclude that a novel object (such as a type of vehicle it did not see during training) is an entirely other type of object, likely the closest match visually to any object type that was seen during training. It may, for example, predict the novel vehicle is a billboard, phone pole, or another unmoving object. But if an outlier detector, running in parallel, recognizes that this object is unusual (and likely out-of-distribution, OOD), the system as a whole can adapt a more conservative and cautious approach to the object and any relevant fail-safe mechanisms in place can be activated.
Another common use of outlier detection with image data is in medical imaging, where anything unusual appearing in images may be a concern and worth further investigation. Again, we are not interested in unusual properties of the image itself — only if any of the objects in the images are OOD: unlike anything seen during training (or only rarely seen during training) and therefore rare and possibly an issue.
Other examples are detecting where unusual objects appear in security cameras, or in cameras monitoring industrial processes. Again, anything unusual is likely worth taking note of.
With self-driving cars, detecting OOD objects may allow the team to enhance its training data. With medical imaging or industrial processes, very often anything unusual is a risk of being a problem. And, as with cars, just knowing we’ve detected an OOD object allows the system to be more conservative and not assume the classification predictions are correct.
As detecting OOD objects in images is key to outlier detection in vision, often the training and testing done relates specifically to this. Often with image data, an outlier detection system is trained on images from one data collection, and testing is done using another similar dataset, with the assumption that the images are different enough to be considered to be from a different distribution (and contain different types of object). This, then, tests the ability to detect OOD data.
For example, training may be done using a set of images covering, say, 100 types of bird, with testing done using another set of images of birds. We generally assume that, if different sources for the images are used, any images from the second set will be at least slightly different and may be assumed to be out-of-distribution, though labels may be used to qualify this better as well: if the training set contains, say, European Greenfinch and the test set does as well, it is reasonable to consider these as not OOD.
Autoencoders
To start to look more specifically at how outlier detection can be done with neural networks, we’ll look first at one of the most practical and straightforward methods, autoencoders. There’s more thorough coverage in Outlier Detection in Python, as well as coverage of VAEs, GANs, and the variations of these available in different packages, but this will give some introduction to at least one means to perform outlier detection.
As indicated, autoencoders are a form of neural network that were traditionally used as a compression tool, though they have been found to be useful for outlier detection as well. Auto encoders take input and learn to compress this with as little loss as possible, such that it can be reconstructed to be close to the original. For tabular data, autoencoders are given one row at a time, with the input neurons corresponding to the columns of the table. For image data, they are given one image at a time, with the input neurons corresponding to the pixels of the picture (though images may also be given in an embedding format).
The figure below provides an example of an autoencoder. This is a specific form of a neural network that is designed not to predict a separate target, but to reproduce the input given to the autoencoder. We can see that the network has as many elements for input (the left-most neurons of the network, shown in orange) as for output (the right-most neurons of the network, shown in green), but in between, the layers have fewer neurons. The middle layer has the fewest; this layer represents the embedding (also known as the bottleneck, or the latent representation) for each object.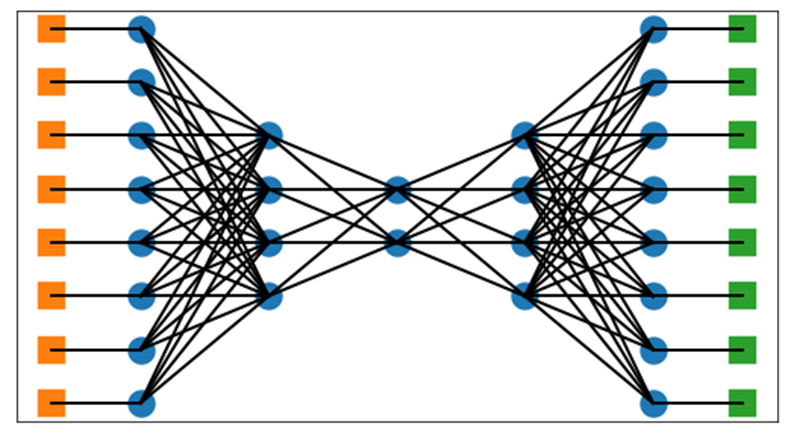
The size of the middle layer is the size to which we attempt to compress all data, such that it can be recreated (or almost recreated) in the subsequent layers. The embedding created is essentially a concise vector of floating-point numbers that can represent each item.
Autoencoders have two main parts: the first layers of the network are known as the encoder. These layers shrink the data to progressively fewer neurons until they reach the middle of the network. The second part of the network is known as the decoder: a set of layers symmetric with the encoder layers that take the compressed form of each input and attempt to reconstruct it to its original form as closely as possible.
If we are able to train an autoencoder that tends to have low reconstruction error (the output of the network tends to match the input very closely), then if some records have high reconstruction error, they are outliers — they do not follow the general patterns of the data that allow for the compression.
Compression is possible because there are typically some relationships between the features in tabular data, between the words in text, between the concepts in images, and so on. When items are typical, they follow these patterns, and the compression can be quite effective (with minimal loss). When items are atypical, they do not follow these patterns and cannot be compressed without more significant loss.
The number and size of the layers is a modeling decision. The more the data contains patterns (regular associations between the features), the more we are able to compress the data, which means the fewer neurons we can use in the middle layer. It usually takes some experimentation, but we want to set the size of the network so that most records can be constructed with very little, but some, error.
If most records can be recreated with zero error, the network likely has too much capacity — the middle layer is able to fully describe the objects being passed through. We want any unusual records to have a larger reconstruction error, but also to be able to compare this to the moderate error we have with typical records; it’s hard to gauge how unusual a record’s reconstruction error is if almost all other records have an error of 0.0. If this occurs, we know we need to scale back the capacity of the model (reduce the number or neurons) until this is no longer possible. This can, in fact, be a practical means to tune the autoencoder — starting with, for example, many neurons in the middle layers and then gradually adjusting the parameters until you get the results you want.
In this way, autoencoders are able to create an embedding (compressed form of the item) for each object, but we typically do not use the embedding outside of this autoencoder; the outlier scores are usually based entirely on the reconstruction error.
This is not always the case though. The embeddings created in the middle layer are legitimate representations of the objects and can be used for outlier detection. The figure below shows an example where we use two neurons for the middle layer, which allows plotting the latent space as a scatter plot. The x dimension represents the values appearing in one neuron and the y dimension in the other neuron. Each point represents the embedding of an object (possibly an image, sound clip, document, or a table row).
Any standard outlier detector (e.g. KNN, Isolation Forest, Convex Hull, Mahalanobis distance, etc.) can then be used on the latent space. This provides an outlier detection system that is somewhat interpretable if limited to two or three dimensions, but, as with principal component analysis (PCA) and other dimensionality reduction methods, the latent space itself is not interpretable.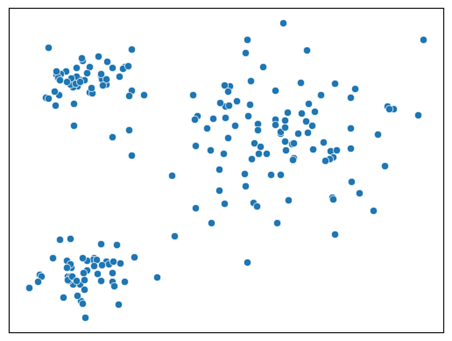
Assuming we use the reconstruction error to identify outliers, to calculate the error, any distance metric may be used to measure the distance between the input vector and the output vector. Often Cosine, Euclidean or Manhattan distances are used, with a number of others being fairly common as well. In most cases, it is best to standardize the data before performing outlier detection, both to allow the neural network to fit better and to measure the reconstruction error more fairly. Given this, the outlier score of each record can be calculated as the reconstruction error divided by the median reconstruction error (for some reference dataset).
Another approach, which can be more robust, is to not use a single error metric for the reconstruction, but to use several. This allows us to effectively use the autoencoder to generate a set of features for each record (each relating to a measurement of the reconstruction error) and pass this to a standard outlier detection tool, which will find the records with unusually large values given by one or more reconstruction error metrics.
In general, autoencoders can be an effective means to locate outliers in data, even where there are many features and the outliers are complex — for example with tabular data, spanning many features. One challenge of autoencoders is they do require setting the architecture (the number of layers of the network and the number of neurons per layer), as well as many parameters related to the network (the activation method, learning rate, dropout rate, and so on), which can be difficult to do.
Any model based on neural networks will necessarily be more finicky to tune than other models. Another limitation of AEs is they may not be appropriate with all types of outlier detection. For example, with image data, they will measure the reconstruction at the pixel level (at least if pixels are used as the input), which may not always be relevant.
Interestingly, GANs can perform better in this regard. The general approach to apply GANs to outlier detection is in some ways similar, but a little more involved. The main idea here, though, is that such deep networks can be used effectively for outlier detection, and that they work similarly for any modality of data, though different detectors will flag different types of outliers, and these may be of more or less interest than other outliers.
Self-supervised Learning for Image Data
As indicated, self-supervised learning (SSL) is another technique for outlier detection with image data (and all other types of data), and is also worth taking a look at.
You’re possibly familiar SSL already if you’re used to working with deep learning in other contexts. It’s quite standard for most areas of deep learning, including where the large neural networks are ultimately used for classification, regression, generation, or other tasks. And, if you’re familiar at all with large language models, you’re likely familiar with the idea of masking words within a piece of text and training a neural network to guess the masked word, which is a form of SSL.
The idea, when working with images, is that we often have a very large collection of images, or can easily acquire a large collection online. In practice we would normally actually simply use a foundation model that has itself been trained in a self-supervised manner, but in principle we can do this ourselves, and in any case, what we’ll describe here is roughly what the teams creating the foundation models do.
Once we have a large collection of images, these are almost certainly unlabeled, which means they can’t immediately be used to train a model (training a model requires defining some loss function, which requires a ground truth label for each item). We’ll need to assign labels to each of the images in one way or another. One way is to manually label the data, but this is expensive, time-consuming, and error-prone. It’s also possible to use self-supervised learning, and much of the time this is much more practical.
With SSL, we find a way to arrange the data such that it can automatically be labelled in some way. As indicated, masking is one such way, and is very common when training large language models, and the same masking technique can be used with image data. With images, instead of masking a word, we can mask an area of an image (as in the image of a mug below), and train a neural network to guess the content of the masked out areas.
With image data, several other techniques for self-supervised learning are possible as well.
In general, they work on the principle of creating what’s called a proxy task or a pretext task. That is, we train a model to predict something (such as the missing areas of an image) on the pretext that this is what we are interested in, though in fact our goal actually to train a neural network that understands the images. We can also say, the task is a proxy for this goal.
This is important, as there’s no way to specifically train for outlier detection; proxy tasks are necessary. Using these, we can create a foundation model that has a good general understand of images (a good enough understanding that it is able to perform the proxy task). Much like foundation models for language, these models can then be fine-tuned to be used for other tasks. This can include classification, regression and other such tasks, but also outlier detection.
That is, training in this way (creating a label using self-supervised learning, and training on a proxy task to predict this label), can create a strong foundation model — in order to perform the proxy task (for example, estimating the content of the masked areas of the image), it needs to have a strong understanding of the type of images it’s working with. Which also means, it may be well set up to identify anomalies in the images.
The trick with SSL for outlier detection is to identify good proxy tasks, that allow us to create a good representation of the domain we are modelling, and that allows us to reliably identify any meaningful anomalies in the data we have.
With image data, there are many opportunities to define useful pretext tasks. We have a large advantage that we don’t have with many other modalities: if we have a picture of an object, and we distort the image in any way, it’s still an image of that same object. And, as indicated, it’s most often the object that we’re interested in, not the picture. This allows us to perform many operations on the images that can support, even if indirectly, our final goal of outlier detection.
Some of these include: rotating the image, adjusting the colours, cropping, and stretching, along with other such perturbations of the images. After performing these transformations, the image may look quite different, and at the pixel level, it is quite different, but the object that is shown is the same.
This opens up at least a couple of methods for outlier detection. One is to take advantage of these transformations to create embeddings for the images and identify the outliers as those with unusual embeddings. Another is to use the transformations more directly. I’ll describe both of these in the next sections.
Creating embeddings and using feature modeling
There are quite a number of ways to create embeddings for images that may be useful for outlier detection. I’ll describe one here called contrastive learning.
This takes advantage of the fact that perturbed versions of the same image will represent the same object and so should have similar embeddings. Given that, we can train a neural network to, given two or more variations of the same image, give these similar embeddings, while assigning different embeddings to different images. This encourages the neural network to focus on the main object in each image and not the image itself, and to be robust to changes in colour, orientation, size, and so on.
But, contrastive learning is merely one means to create embeddings for images, and many others, including any self-supervised means, may work best for any given outlier detection task.
Once we have embeddings for the images, we can identify the objects with unusual embeddings, which will be the embeddings unusually far from most other embeddings. For this, we can use the Euclidean, cosine, or other distance measures between the images in the embedding space.
An example of this with tabular data is covered in the next article in this series.
Using the pretext tasks directly
What can also be interesting and quite effective is to use the perturbations more directly to identify the outliers. As an example, consider rotating an image.
Given an image, we can rotate it 0, 90, 180, and 270 degrees, and so then have four versions of the same image. We can then train a neural network to predict, given any image, if it was rotated 0, 90, 180, or 270 degrees. As with some of the examples above (where outliers may be items that do not fit into clusters well, do not contain the frequent item patterns, do not compress well, and so on), here outliers are the images where the neural network cannot predict well how much each version of the image was rotated.
With typical images, when we pass the four variations of the image through the network (assuming the network was well-trained), it will tend to predict the rotation of each of these correctly, but with atypical images, it will not be able to predict accurately, or will have lower confidence in the predictions.
The same general approach can be used with other perturbations, including flipping the image, zooming in, stretching, and so on — in these examples the model predicts how the image was flipped, the scale of the image, or how it was stretched.
Some of these may be used for other modalities as well. Masking, for example, may be used with virtually any modality. Some though, are not as generally applicable; flipping, for example, may not be effective with audio data.
Techniques for outlier detection with image data
I’ll recap here what some of the most common options are:
- Autoencoders, variational autoencoders, and Generative Adversarial networks. These are well-established and quite likely among the most common methods for outlier detection.
- Feature modeling — Here embeddings are created for each object and standard outlier detection (e.g., Isolation Forest, Local Outlier Factor (LOF), k-Nearest Neighbors (KNN), or a similar algorithm) is used on the embeddings. As discussed in the next article, embeddings created to support classification or regression problems do not typically tend to work well in this situation, but we look later at some research related to creating embeddings that are more suitable for outlier detection.
- Using the pretext tasks directly. For example, predicting the rotation, stretching, scaling, etc. of an image. This is an interesting approach, and may be among the most useful for outlier detection.
- Confidence scores — Here we consider where a classifier is used, and the confidence associated with all classes is low. If a classifier was trained to identify, say, 100 types of birds, then it will, when presented with a new image, generate a probability for each of those 100 types of bird. If the probability for all these is very low, the object is unusual in some way and quite likely out of distribution. As indicated, classifiers often provide high confidences even when incorrect, and so this method isn’t always reliable, but even where it is not, when low confidence scores are returned, a system can take advantage of this and recognize that the image is unusual in some regard.
Neural networks with image data
With image data, we are well-positioned to take advantage of deep neural networks, which can create very sophisticated models of the data: we have access to an extremely large body of data, we can use tools such as autoencoders, VAEs and GANS, and self-supervised learning is quite feasible.
One of the important properties of deep neural networks is that they can be grown to very large sizes, which allows them to take advantage of additional data and create even more sophisticated models.
This is in distinction from more traditional outlier detection models, such as Frequent Patterns Outlier Factor (FPOF), association rules, k-Nearest Neighbors, Isolation Forest, LOF, Radius, and so on: as they train on additional data, they may develop slightly more accurate models of normal data, but they tend to level off after some time, with greatly diminishing returns from training with additional data beyond some point. Deep learning models, on the other hand, tend to continue to take advantage of access to more data, even after huge amounts of data have already been used.
We should note, though, that although there has been a great deal of progress in outlier detection with images, it is not yet a solved problem. It is much less subjective than with other modalities, at least where it is defined to deal strictly with out-of-distribution data (though it is still somewhat vague when an object really is of a different type than the objects seen during training — for example, with birds, if a Jay and a Blue Jay are distinct categories). Image data is challenging to work with, and outlier detection is still a challenging area.
Tools for deep learning-based outlier detection
There are several tools that may be used for deep learning-based outlier detection. Three of these, which we’ll look at here and in the next article, are are PyOD, DeepOD, and Alibi-Detect.
PyOD, I’ve covered in some previous articles, and is likely the most comprehensive tool available today for outlier detection on tabular data in python. It contains several standard outlier detectors (Isolation Forest, Local Outlier Factor, Kernel Density Estimation (KDE), Histogram-Based Outlier-Detection (HBOS), Gaussian Mixture Models (GMM), and several others), as well as a number of deep learning-based models, based on autoencoders, variation autoencoders, GANS, and variations of these.
DeepOD provides outlier detection for tabular and time series data. I’ll take a closer look at this in the next article.
Alibi-Detect covers outlier detection for tabular, time-series, and image data. An example of this with image data is shown below.
Most deep learning work today is based on either TensorFlow/Keras or PyTorch (with PyTorch gaining an increasingly large share). Similarly, most deep learning-based outlier detection uses one or the other of these.
PyOD is probably the most straight-forward of these three libraries, at least in my experience, but all are quite manageable and well-documented.
Example using PyOD
This section shows an example using PyOD’s AutoEncoder outlier detector for a tabular dataset (specifically the KDD dataset, available with a public license).
Before using PyOD, it’s necessary to install it, which may be done with:
pip install pyod
You’ll then need to install either TensorFlow or PyTorch if they’re not already installed (depending which detector is being used). I used Google colab for this, which has both TensorFlow & PyTorch installed already. This example uses PyOD’s AutoEncoder outlier detector, which uses PyTorch under the hood.
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_kddcup99
from pyod.models.auto_encoder import AutoEncoder
# Load the data
X, y = fetch_kddcup99(subset="SA", percent10=True, random_state=42,
return_X_y=True, as_frame=True)
# Convert categorical columns to numeric, using one-hot encoding
cat_columns = ["protocol_type", "service", "flag"]
X = pd.get_dummies(X, columns=cat_columns)
det = AutoEncoder()
det.fit(X)
scores = det.decision_scores_
Although an autoencoder is more complicated than many of the other detectors supported by PyOD (for example, HBOS is based in histograms, Cook’s Distance on linear regression; some others are also relatively simple), the interface to work with the autoencoder detector in PyOD is just as simple. This is especially true where, as in this example, we use the default parameters. The same is true for detectors provided by PyOD based on VAEs and GANs, which are, under the hood, even a little more complex than autoencoders, but the API, other than the parameters, is the same.
In this example, we simply load in the data, convert the categorical columns to numeric format (this is necessary for any neural-network model), create an AutoEncoder detector, fit the data, and evaluate each record in the data.
Alibi-Detect
Alibi-Detect also supports autoencoders for outlier detection. It does require some more coding when creating detectors than PyOD; this can be slightly more work, but also allows more flexibility. Alibi-Detect’s documentation provides several examples, which are useful to get you started.
The listing below provides one example, which can help explain the general idea, but it is best to read through their documentation and examples to get a thorough understanding of the process. The listing also uses an autoencoder outlier detector. As alibi-detect can support image data, we provide an example using this.
Working with deep neural networks can be slow. For this, I’d recommend using GPUs if possible. For example, some of the examples found on Alibi-Detect’s documentation, or variations on these I’ve tested, may take about 1 hour on Google colab using a CPU runtime, but only about 3 minutes using the T4 GPU runtime.
Example of Outlier Detection for Image Data
For this example, I just provide some generic code that can be used for any dataset, though the dimensions of the layers will have to be adjusted to match the size of the images used. This example just calls a undefined method called load_data() to get the relevant data (the next example looks closer at specific dataset — here I’m just showing the general system Alibi-Detect uses).
This example starts by first using Keras (if you’re more familiar with PyTorch, the ideas are similar when using Keras) to create the encoder and decoders used by the autoencoder, and then passing these as parameters to the OutlierAE object alibi-detect provides.
As is common with image data, the neural network includes convolutional layers. These are used at times with other types of data as well, including text and time series, though rarely with tabular. It also uses a dense layer.
The code assumes the images are 32x32. With other sizes, the decoder must be organized so that it outputs images of this size as well. The OutlierAE class works by comparing the input images to the the output images (after passing the input images through both the encoder and decoder), so the output images must have identical sizes as the input. This is a bit more finicky when using Conv2D and Conv2DTranspose layers, as in this example, than when using dense layers.
We then call fit() and predict(). For fit(), we specify five epochs. Using more may work better but will also require more time. Alibi-detect’s OutlierAE uses the reconstruction error (specifically, the mean squared error of the reconstructed image from the original image).
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
tf.keras.backend.clear_session()
from tensorflow.keras.layers import Conv2D, Conv2DTranspose, \
Dense, Layer, Reshape, InputLayer, Flatten
from alibi_detect.od import OutlierAE
# Loads the data used
train, test = load_data()
X_train, y_train = train
X_test, y_test = test
X_train = X_train.astype('float32') / 255
X_test = X_test.astype('float32') / 255
encoding_dim = 1024
# Defines the encoder portion of the AE
encoder_net = tf.keras.Sequential([
InputLayer(input_shape=(32, 32, 3)),
Conv2D(64, 4, strides=2, padding='same', activation=tf.nn.relu),
Conv2D(128, 4, strides=2, padding='same', activation=tf.nn.relu),
Conv2D(512, 4, strides=2, padding='same', activation=tf.nn.relu),
Flatten(),
Dense(encoding_dim,)])
# Defines the decoder portion of the AE
decoder_net = tf.keras.Sequential([
InputLayer(input_shape=(encoding_dim,)),
Dense(4*4*128),
Reshape(target_shape=(4, 4, 128)),
Conv2DTranspose(256, 4, strides=2, padding='same',
activation=tf.nn.relu),
Conv2DTranspose(64, 4, strides=2, padding='same',
activation=tf.nn.relu),
Conv2DTranspose(3, 4, strides=2, padding='same',
activation='sigmoid')])
# Specifies the threshold for outlier scores
od = OutlierAE(threshold=.015,
encoder_net=encoder_net,
decoder_net=decoder_net)
od.fit(X_train, epochs=5, verbose=True)
# Makes predictions on the records
X = X_train
od_preds = od.predict(X,
outlier_type='instance',
return_feature_score=True,
return_instance_score=True)
print("Number of outliers with normal data:",
od_preds['data']['is_outlier'].tolist().count(1))
This makes predictions on the rows used from the training data. Ideally, none are outliers.
Example using PyTorch
As autoencoders are fairly straightforward to create, this is often done directly, as well as with tools such as Alibi-Detect or PyOD. In this example we work with the MNIST dataset (available with a public license, in this case distributed with PyTorch’s torchvision) and show a quick example using PyTorch.
import numpy as np
import torch
from torchvision import datasets, transforms
from matplotlib import pyplot as plt
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision.utils import make_grid
# Collect the data
train_dataset = datasets.MNIST(root='./mnist_data/', train=True,
transform=transforms.ToTensor(), download=True)
test_dataset = datasets.MNIST(root='./mnist_data/', train=False,
transform=transforms.ToTensor(), download=True)
# Define DataLoaders
batchSize=128
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batchSize, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batchSize, shuffle=False)
# Display a sample of the data
inputs, _ = next(iter(test_loader))
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(12, 4))
for i in range(10):
ax[i].imshow(inputs[i][0])
plt.tight_layout()
plt.show()
# Define the properties of the autoencoder
num_input_pixels = 784
num_neurons_1 = 256
num_neurons_2 = 64
# Define the Autoencoder
class Autoencoder(nn.Module):
def __init__(self, x_dim, h_dim1, h_dim2):
super(Autoencoder, self).__init__()
# Encoder
self.layer1 = nn.Linear(x_dim, h_dim1)
self.layer2 = nn.Linear(h_dim1, h_dim2)
# Decoder
self.layer3 = nn.Linear(h_dim2, h_dim1)
self.layer4 = nn.Linear(h_dim1, x_dim)
def encoder(self, x):
x = torch.sigmoid(self.layer1(x))
x = torch.sigmoid(self.layer2(x))
return x
def decoder(self, x):
x = torch.sigmoid(self.layer3(x))
x = torch.sigmoid(self.layer4(x))
return x
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
model = Autoencoder(num_input_pixels, num_neurons_1, num_neurons_2)
model.cuda()
optimizer = optim.Adam(model.parameters())
n_epoch = 20
loss_function = nn.MSELoss()
for i in range(n_epoch):
train_loss = 0
for batch_idx, (data, _) in enumerate(train_loader):
data = data.cuda()
inputs = torch.reshape(data,(-1, 784))
optimizer.zero_grad()
# Get the result of passing the input through the network
recon_x = model(inputs)
# The loss is in terms of the difference between the input and
# output of the model
loss = loss_function(recon_x, inputs)
loss.backward()
train_loss += loss.item()
optimizer.step()
if i % 5 == 0:
print(f'Epoch: {i:>3d} Average loss: {train_loss:.4f}')
print('Training complete...')
This example uses cuda, but this can be removed where no GPU is available.
In this example, we collect the data, create a DataLoader for the train and for the test data (this is done with most projects using PyTorch), and show a sample of the data, which we see here:
The data contains hand-written digits.
We next define an autoencoder, which defines the encoder and decoder both clearly. Any data passed through the autoencoder goes through both of these.
The autoencoder is trained in a manner similar to most neural networks in PyTorch. We define an optimizer and loss function, and iterate over the data for a certain number of epochs (here using 20), each time covering the data in some number of batches (this uses a batch size of 128, so 16 batches per epoch, given the full data size). After each batch, we calculate the loss, which is based on the difference between the input and output vectors, then update the weights, and continue.
Executing the following code, we can see that with most digits, the reconstruction error is very small:
inputs, _ = next(iter(test_loader))
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(12, 4))
for i in range(10):
ax[i].imshow(inputs[i][0])
plt.tight_layout()
plt.show()
inputs=inputs.cuda()
inputs=torch.reshape(inputs,(-1,784))
outputs=model(inputs)
outputs=torch.reshape(outputs,(-1,1,28,28))
outputs=outputs.detach().cpu()
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(12, 4))
for i in range(10):
ax[i].imshow(outputs[i][0])
plt.tight_layout()
plt.show()


We can then test with out-of-distribution data, passing in this example a character close to an X (so unlike any of the 10 digits it was trained on).
inputs, _ = next(iter(test_loader))
for i in range(28):
for j in range(28):
inputs[0][0][i][j] = 0
if i == j:
inputs[0][0][i][j] = 1
if i == j+1:
inputs[0][0][i][j] = 1
if i == j+2:
inputs[0][0][i][j] = 1
if j == 27-i:
inputs[0][0][i][j] = 1
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(12, 4))
for i in range(10):
ax[i].imshow(inputs[i][0])
plt.tight_layout()
plt.show()
inputs=inputs.cuda()
inputs=torch.reshape(inputs,(-1,784))
outputs=model(inputs)
outputs=torch.reshape(outputs,(-1,1,28,28))
outputs=outputs.detach().cpu()
fig, ax = plt.subplots(nrows=1, ncols=10, figsize=(12, 4))
for i in range(10):
ax[i].imshow(outputs[i][0])
plt.tight_layout()
plt.show()
This outputs:

In this case, we see that the reconstruction error for the X is not huge — it’s able to recreate what looks like an X, but the error is unusually large relative to the other characters.
Deep learning-based outlier detection with tabular data
In order to keep this article a manageable length, I’ll wrap up here and continue with tabular data in the next article. For now I’ll just recap that the methods above (or variations of them) can be applied to tabular data, but that there are some significant differences with tabular data that make these techniques more difficult. For example, it’s difficult to create embeddings to represent table records that are more effective for outlier detection than simply using the original records.
As well, the transformations that may be applied to images do not tend to lend themselves well to table records. When perturbing an image of a given object, we can be confident that the new image is still an image of the same object, but when we perturb a table record (especially without strong domain knowledge), we cannot be confident that it’s semantically the same before and after the perturbation. We will, though, look in the next article at techniques to work with tabular data that is often quite effective, and some of the tools available for this.
I’ll also go over, in the next article, challenges with using embeddings for outlier detection, and techniques to make them more practical.
Conclusions
Deep learning is necessary for outlier detection with many modalities including image data, and is showing promise for other areas where it is not yet as well-established, such as tabular data. At present, however, more traditional outlier detection methods still tend to work best for tabular data.
Having said that, there are cases now where deep learning-based outlier detection can be the most effective method for identifying anomalies in tabular data, or at least can be useful to include among the methods examined (and possibly included in a larger ensemble of detectors).
There are many approaches to using deep learning for outlier detection, and we’ll probably see more developed in coming years. Some of the most established are autoencoders, variational autoencoders, and GANs, and there is good support for these in the major outlier detection libraries, including PyOD and Alibi-Detect.
Self-supervised learning for outlier detection is also showing a great deal of promise. We’ve covered here how it can be applied to image data, and cover tabular data in the next article. It can, as well, be applied, in one form or another, to most modalities. For example, with most modalities, there’s usually some way to implement masking, where the model learns to predict the masked portion of the data. For instance, with time series data, the model can learn to predict the masked values in a range, or set of ranges, within a time series.
As well as the next article in this series (which will cover deep learning for tabular data, and outlier detection with embeddings), in the coming articles, I’ll try to continue to cover traditional outlier detection, including for tabular and time series data, but will also cover more deep-learning based methods (including more techniques for outlier detection, more descriptions of the existing tools, and more coverage of other modalities).
All images by author
Deep Learning for Outlier Detection on Tabular and Image Data was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.


 Editor-Admin
Editor-Admin 





