Building a Regression Model: Delivery Duration Prediction
Building a Regression Model to Predict Delivery Durations: A Practical GuideE2E walkthrough for approaching a regression modeling taskIn this article, we’re going to walk through the process of building a regression model — from dataset cleaning & preparation, to model training & evaluation. The specific regression task we will model for is predicting the expected delivery time for a food delivery service.Comprehensive information about the project & the dataset involved can be found here.If you want to follow along with the analysis, you can find the original notebooks in the GitHub here.ContentsBackgroundDataset InfoHigh-Level ApproachData Preparation & Exploratory AnalysisBuilding ModelsFinal Model EvaluationConclusionSourcesBackgroundTo provide some motivation for this task, let’s assume we are working for some food delivery service, such as DoorDash.When a customer places an order on DoorDash, DoorDash must display the estimated amount of time it will take until the customer receives their order. Predicting this arrival time accurately is crucial for DoorDash’s customer satsifaction:If DoorDash cannot track a customer’s order status precisely, naturally customers will not want to order using the app as they will have no idea when they will receive their order.Thus, our goal is to build a regression model that can predict this delivery time accurately. Precisely, the delivery time is defined as the time elapsed between the moment a customer places an order to when the customer receives their order. To accomplish this goal, we are provided some historical orders data, which we describe below.Dataset InfoThe data we are working with contains historical DoorDash orders data from early 2015 in a subset of the cities in which they operate.The data includes features related to the following: order details (price, number of items, etc.), market conditions at the time the order was placed (e.g. # of available drivers), and ingredients for our prediction target (timestamp when order was placed & when it was delivered).The full data dictionary can be found in the project link.High-Level ApproachBuilding a regression model from scratch is an extensive process that requires some trial & error. Essentially, the general approach we will take looks something like this:Data prep & exploration (data exploration, cleaning, feature engineering).Model building/experimentation (train, tune, and compare several different regression algorithms).Final model selection & evaluation (choose the “best” model from our experiments, and evaluate it on our holdout set).Additionally, data preparation & exploration can be broken down further into the following steps:Minimal dataset exploration/cleaning (just enough to check whether any features should be dropped or any observations should be removed, create prediction target).Split into train/test (we do not want to explore the feature distributions of the specific observations that we will evaluate our final model upon).More dataset exploration/cleaning (check feature distributions & their relations with the prediction target, decide how to deal with missing values accordingly, explore relationships between features).Feature engineering (derive new features from the existing feature set that may help predict delivery duration).In practice, there may be some back & forth between these steps (features highlighted as important during model training may motivate additional feature engineering related to those features, or poor model performance may motivate the need to gather more data). For now, we’ll walk through this task following the process above.Data Preparation & Exploratory AnalysisNow that we’ve outlined our approach, let’s take a look at our data and what kind of features we’re working with.From the above, we see our data contains ~197,000 deliveries, with a variety of numeric & non-numeric features. None of the features are missing a large percentage of values (lowest non-null count ~181,000), so we likely won’t have to worry about dropping any features entirely.Let’s check if our data contains any duplicated deliveries, and if there are any observations that we cannot compute delivery time for.print(f"Number of duplicates: {df.duplicated().sum()} \n")print(pd.DataFrame({'Missing Count': df[['created_at', 'actual_delivery_time']].isna().sum()}))We see that all the deliveries are unique. However, there are 7 deliveries that are missing a value for actual_delivery_time, which means we won’t be able to compute the delivery duration for these orders. Since there’s only a handful of these, we’ll remove these observations from our data.Now, let’s create our prediction target. We want to predict the delivery duration (in seconds), which is the elapsed time between when the customer placed the order (‘created_at’) and when they recieved the order (‘actual_delivery_time’).# convert columns to datetime df['created_at'] = pd.to_datetime(df['created_at'], utc=True)df['actual_delivery_time'

Building a Regression Model to Predict Delivery Durations: A Practical Guide
E2E walkthrough for approaching a regression modeling task
In this article, we’re going to walk through the process of building a regression model — from dataset cleaning & preparation, to model training & evaluation. The specific regression task we will model for is predicting the expected delivery time for a food delivery service.
Comprehensive information about the project & the dataset involved can be found here.
If you want to follow along with the analysis, you can find the original notebooks in the GitHub here.
Contents
- Background
- Dataset Info
- High-Level Approach
- Data Preparation & Exploratory Analysis
- Building Models
- Final Model Evaluation
- Conclusion
- Sources
Background
To provide some motivation for this task, let’s assume we are working for some food delivery service, such as DoorDash.
When a customer places an order on DoorDash, DoorDash must display the estimated amount of time it will take until the customer receives their order. Predicting this arrival time accurately is crucial for DoorDash’s customer satsifaction:
- If DoorDash cannot track a customer’s order status precisely, naturally customers will not want to order using the app as they will have no idea when they will receive their order.
- Thus, our goal is to build a regression model that can predict this delivery time accurately. Precisely, the delivery time is defined as the time elapsed between the moment a customer places an order to when the customer receives their order. To accomplish this goal, we are provided some historical orders data, which we describe below.
Dataset Info
- The data we are working with contains historical DoorDash orders data from early 2015 in a subset of the cities in which they operate.
- The data includes features related to the following: order details (price, number of items, etc.), market conditions at the time the order was placed (e.g. # of available drivers), and ingredients for our prediction target (timestamp when order was placed & when it was delivered).
- The full data dictionary can be found in the project link.
High-Level Approach
Building a regression model from scratch is an extensive process that requires some trial & error. Essentially, the general approach we will take looks something like this:
- Data prep & exploration (data exploration, cleaning, feature engineering).
- Model building/experimentation (train, tune, and compare several different regression algorithms).
- Final model selection & evaluation (choose the “best” model from our experiments, and evaluate it on our holdout set).
Additionally, data preparation & exploration can be broken down further into the following steps:
- Minimal dataset exploration/cleaning (just enough to check whether any features should be dropped or any observations should be removed, create prediction target).
- Split into train/test (we do not want to explore the feature distributions of the specific observations that we will evaluate our final model upon).
- More dataset exploration/cleaning (check feature distributions & their relations with the prediction target, decide how to deal with missing values accordingly, explore relationships between features).
- Feature engineering (derive new features from the existing feature set that may help predict delivery duration).
In practice, there may be some back & forth between these steps (features highlighted as important during model training may motivate additional feature engineering related to those features, or poor model performance may motivate the need to gather more data). For now, we’ll walk through this task following the process above.
Data Preparation & Exploratory Analysis
Now that we’ve outlined our approach, let’s take a look at our data and what kind of features we’re working with.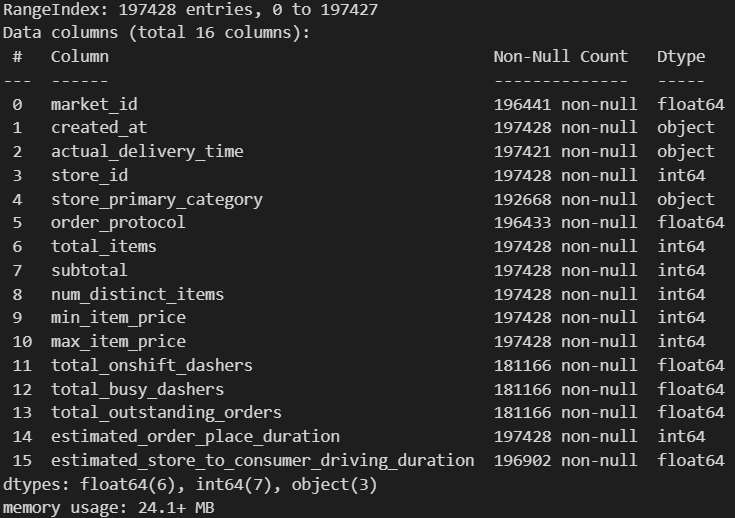
From the above, we see our data contains ~197,000 deliveries, with a variety of numeric & non-numeric features. None of the features are missing a large percentage of values (lowest non-null count ~181,000), so we likely won’t have to worry about dropping any features entirely.
Let’s check if our data contains any duplicated deliveries, and if there are any observations that we cannot compute delivery time for.
print(f"Number of duplicates: {df.duplicated().sum()} \n")
print(pd.DataFrame({'Missing Count': df[['created_at', 'actual_delivery_time']].isna().sum()}))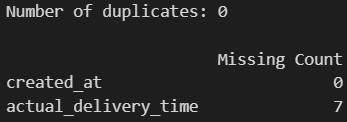
We see that all the deliveries are unique. However, there are 7 deliveries that are missing a value for actual_delivery_time, which means we won’t be able to compute the delivery duration for these orders. Since there’s only a handful of these, we’ll remove these observations from our data.
Now, let’s create our prediction target. We want to predict the delivery duration (in seconds), which is the elapsed time between when the customer placed the order (‘created_at’) and when they recieved the order (‘actual_delivery_time’).
# convert columns to datetime
df['created_at'] = pd.to_datetime(df['created_at'], utc=True)
df['actual_delivery_time'] = pd.to_datetime(df['actual_delivery_time'], utc=True)
# create prediction target
df['seconds_to_delivery'] = (df['actual_delivery_time'] - df['created_at']).dt.total_seconds()
The last thing we’ll do before splitting our data into train/test is check for missing values. We already viewed the non-null counts for each feature above, but let’s view the proportions to get a better picture.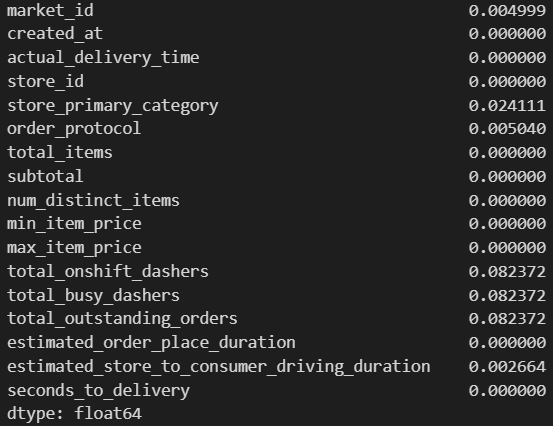
We see that the market features (‘onshift_dashers’, ‘busy_dashers’, ‘outstanding_orders’) have the highest percentage of missing values (~8% missing). The feature with the second-highest missing data rate is ‘store_primary_category’ (~2%). All other features have < 1% missing.
Since none of the features have a high missing count, we won’t remove any of them. Later on, we will look at the feature distributions to help us decide how to appropriately deal with missing observations for each feature.
But first, let’s split our data into train/test. We will proceed with an 80/20 split, and we’ll write this test data to a separate file which we won’t touch until evaluating our final model.
from sklearn.model_selection import train_test_split
import os
# shuffle
df = df.sample(frac=1, random_state=42)
df = df.reset_index(drop=True)
# split
train_df, test_df = train_test_split(df, test_size=0.2, random_state=42)
# write test data to separate file
directory = 'datasets'
file_name = 'test_data.csv'
file_path = os.path.join(directory, file_name)
os.makedirs(directory, exist_ok=True)
test_df.to_csv(file_path, index=False)
Now, let’s dive into the specifics of our train data. We’ll establish our numeric & categorical features, to make it clear which columns are being referenced in later exploratory steps.
categorical_feats = [
'market_id',
'store_id',
'store_primary_category',
'order_protocol'
]
numeric_feats = [
'total_items',
'subtotal',
'num_distinct_items',
'min_item_price',
'max_item_price',
'total_onshift_dashers',
'total_busy_dashers',
'total_outstanding_orders',
'estimated_order_place_duration',
'estimated_store_to_consumer_driving_duration'
]
Let’s revisit the categorical features with missing values (‘market_id’, ‘store_primary_category’, ‘order_protocol’). Since there was little missing data among those features (< 3%), we will simply impute those missing values with an “unknown” category.
- This way, we won’t have to remove data from other features.
- Perhaps the absence of feature values holds some predictive power for delivery duration i.e. these features are not missing at random.
- Additionally, we will add this imputation step to our preprocessing pipeline during modeling, so that we won’t have to manually duplicate this work on our test set.
missing_cols_categorical = ['market_id', 'store_primary_category', 'order_protocol']
train_df[missing_cols_categorical] = train_df[missing_cols_categorical].fillna("unknown")
Let’s look at our categorical features.
pd.DataFrame({'Cardinality': train_df[categorical_feats].nunique()}).rename_axis('Feature')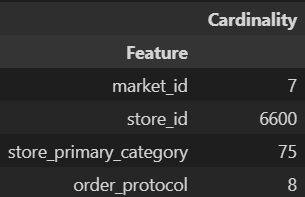
Since ‘market_id’ & ‘order_protocol’ have low cardinality, we can visualize their distributions easily. On the other hand, ‘store_id’ & ‘store_primary_category’ are high cardinality features. We’ll take a deeper look at those later.
import seaborn as sns
import matplotlib.pyplot as plt
categorical_feats_subset = [
'market_id',
'order_protocol'
]
# Set up the grid
fig, axes = plt.subplots(1, len(categorical_feats_subset), figsize=(13, 5), sharey=True)
# Create barplots for each variable
for i, col in enumerate(categorical_feats_subset):
sns.countplot(x=col, data=train_df, ax=axes[i])
axes[i].set_title(f"Frequencies: {col}")
# Adjust layout
plt.tight_layout()
plt.show()
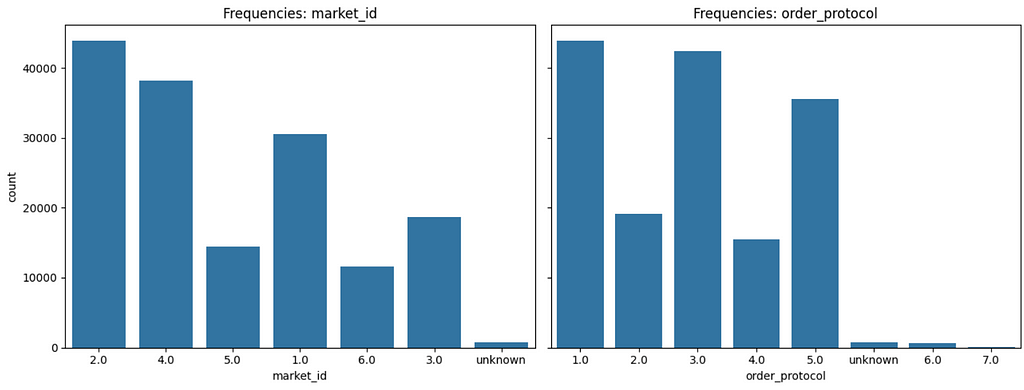
Some key things to note:
- ~70% of orders placed have ‘market_id’ of 1, 2, 4
- < 1% of orders have ‘order_protocol’ of 6 or 7
Unfortunately, we don’t have any additional information about these variables, such as which ‘market_id’ values are associated with which cities/locations, and what each ‘order_protocol’ number represents. At this point, asking for additional data concerning this information may be a good idea, as it may help for investigating trends in delivery duration across broader region/location categorizations.
Let’s look at our higher cardinality categorical features. Perhaps each ‘store_primary_category’ has an associated ‘store_id’ range? If so, we may not need ‘store_id’, as ‘store_primary_category’ would already encapsulate a lot of the information about the store being ordered from.
store_info = train_df[['store_id', 'store_primary_category']]
store_info.groupby('store_primary_category')['store_id'].agg(['min', 'max'])
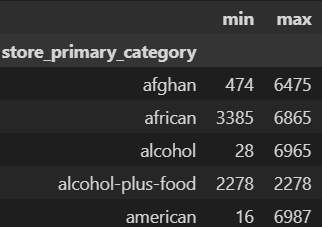
Clearly not the case: we see that ‘store_id’ ranges overlap across levels of ‘store_primary_category’.
A quick look at the distinct values and associated frequencies for ‘store_id’ & ‘store_primary_category’ shows that these features have high cardinality and are sparsely distributed. In general, high cardinality categorical features may be problematic in regression tasks, particularly for regression algorithms that require solely numeric data. When these high cardinality features are encoded, they may enlarge the feature space drastically, making the available data sparse and decreasing the model’s ability to generalize to new observations in that feature space. For a better & more professional explanation of the phenomena, you can read more about it here.
Let’s get a sense of how sparsely distributed these features are.
store_id_values = train_df['store_id'].value_counts()
# Plot the histogram
plt.figure(figsize=(8, 5))
plt.bar(store_id_values.index, store_id_values.values, color='skyblue')
# Add titles and labels
plt.title('Value Counts: store_id', fontsize=14)
plt.xlabel('store_id', fontsize=12)
plt.ylabel('Frequency', fontsize=12)
plt.xticks(rotation=45) # Rotate x-axis labels for better readability
plt.tight_layout()
plt.show()
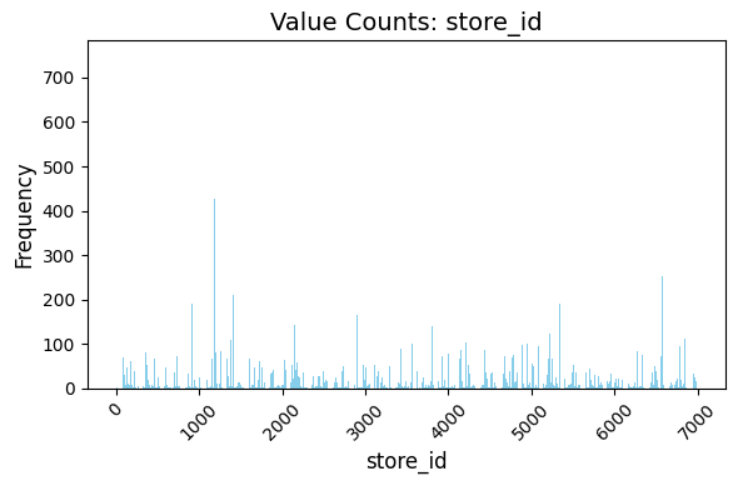
We see that there are a handful of stores that have hundreds of orders, but the majority of them have much less than 100.
To handle the high cardinality of ‘store_id’, we’ll create another feature, ‘store_id_freq’, that groups the ‘store_id’ values by frequency.
- We’ll group the ‘store_id’ values into five different percentile bins shown below.
- ‘store_id_freq’ will have much lower cardinality than ‘store_id’, but will retain relevant information regarding the popularity of the store the delivery was ordered from.
- For more inspiration behind this logic, check out this thread.
def encode_frequency(freq, percentiles) -> str:
if freq < percentiles[0]:
return '[0-50)'
elif freq < percentiles[1]:
return '[50-75)'
elif freq < percentiles[2]:
return '[75-90)'
elif freq < percentiles[3]:
return '[90-99)'
else:
return '99+'
value_counts = train_df['store_id'].value_counts()
percentiles = np.percentile(value_counts, [50, 75, 90, 99])
# apply encode_frequency to each store_id based on their number of orders
train_df['store_id_freq'] = train_df['store_id'].apply(lambda x: encode_frequency(value_counts[x], percentiles))
pd.DataFrame({'Count':train_df['store_id_freq'].value_counts()}).rename_axis('Frequency Bin')
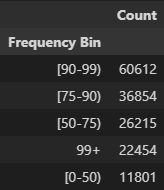
Our encoding shows us that ~60,000 deliveries were ordered from stores catgorized in the 90–99th percentile in terms of popularity, whereas ~12,000 deliveries were ordered from stores that were in the 0–50th percentile in popularity.
Now that we’ve (attempted) to capture relevant ‘store_id’ information in a lower dimension, let’s try to do something similar with ‘store_primary_category’.
Let’s look at the most popular ‘store_primary_category’ levels.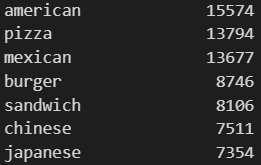
A quick look shows us that many of these ‘store_primary_category’ levels are not exclusive to each other (ex: ‘american’ & ‘burger’). Further investigation shows many more examples of this kind of overlap.
So, let’s try to map these distinct store categories into a few basic, all-encompassing groups.
store_category_map = {
'american': ['american', 'burger', 'sandwich', 'barbeque'],
'asian': ['asian', 'chinese', 'japanese', 'indian', 'thai', 'vietnamese', 'dim-sum', 'korean',
'sushi', 'bubble-tea', 'malaysian', 'singaporean', 'indonesian', 'russian'],
'mexican': ['mexican'],
'italian': ['italian', 'pizza'],
}
def map_to_category_type(category: str) -> str:
for category_type, categories in store_category_map.items():
if category in categories:
return category_type
return "other"
train_df['store_category_type'] = train_df['store_primary_category'].apply(lambda x: map_to_category_type(x))
value_counts = train_df['store_category_type'].value_counts()
# Plot pie chart
plt.figure(figsize=(6, 6))
value_counts.plot.pie(autopct='%1.1f%%', startangle=90, cmap='viridis', labels=value_counts.index)
plt.title('Category Distribution')
plt.ylabel('') # Hide y-axis label for aesthetics
plt.show()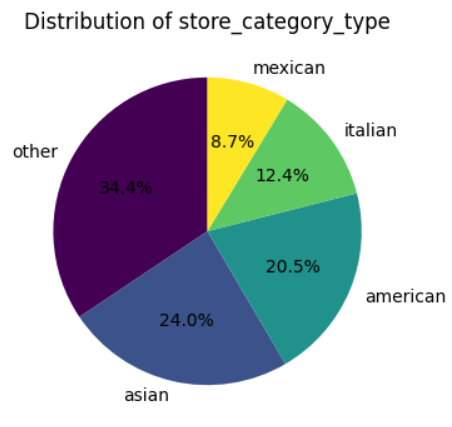
This grouping is probably brutally simple, and there may very well be a better way to group these store categories. Let’s proceed with it for now for simplicity.
We’ve done a good deal of investigation into our categorical features. Let’s look at the distributions for our numeric features.
# Create grid for boxplots
fig, axes = plt.subplots(nrows=5, ncols=2, figsize=(12, 15)) # Adjust figure size
axes = axes.flatten() # Flatten the 5x2 axes into a 1D array for easier iteration
# Generate boxplots for each numeric feature
for i, column in enumerate(numeric_feats):
sns.boxplot(y=train_df[column], ax=axes[i])
axes[i].set_title(f"Boxplot for {column}")
axes[i].set_ylabel(column)
# Remove any unused subplots (if any)
for i in range(len(numeric_feats), len(axes)):
fig.delaxes(axes[i])
# Adjust layout for better spacing
plt.tight_layout()
plt.show()
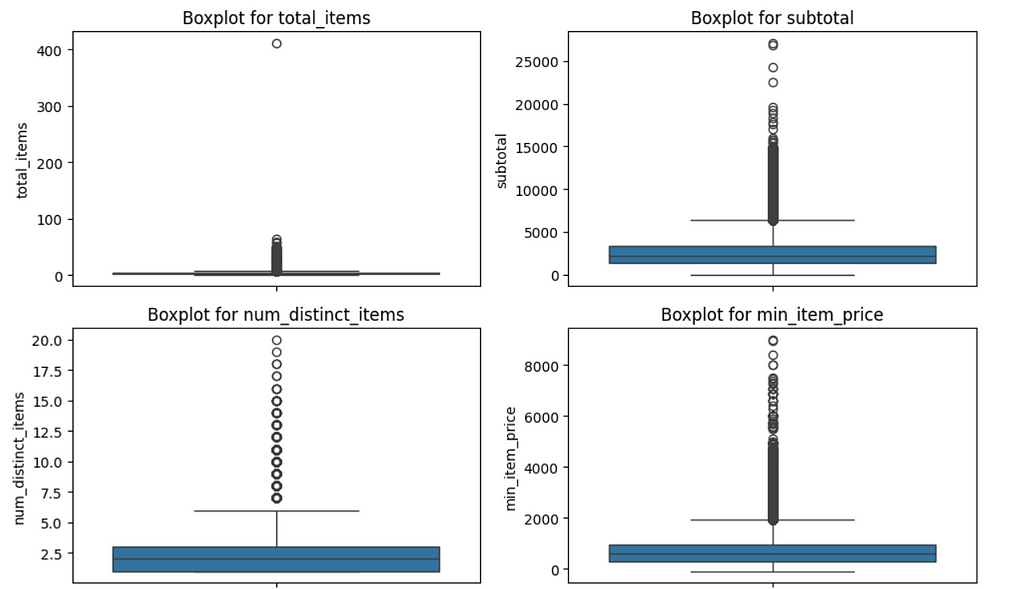
Many of the distributions appear to be more right skewed then they are due to the presence of outliers.
In particular, there seems to be an order with 400+ items. This seems strange as the next largest order is less than 100 items.
Let’s look more into that 400+ item order.
train_df[train_df['total_items']==train_df['total_items'].max()]

That order was a fast-food order that consisted of 411 total items, but only 5 distinct items. It was also placed late at night (midnight-1 am).
While it’s not impossible for somebody to place an order like that (McDonalds late night run??), we’ll proceed to remove this observation from our data since it’s highly unlikely that our model will have to make delivery duration predictions for orders with more than 100 items.
A couple of additional feature engineering steps:
- For each order, we are provided the price of the cheapest (‘min_item_price’) & most expensive (‘max_item_price’) item. We can consolidate this price range information into a single feature, which we’ll call ‘item_price_range’.
- Time of day when the order was placed seems like relevant information for predicting delivery duration — orders placed at times of day when the market is busier are likely to take longer to deliver. So, let’s extract the hour information from the order creation timestamp (‘created_at’). We’ll call this ‘hour_of_day’.
# extract price range
train_df['item_price_range'] = train_df['max_item_price'] - train_df['min_item_price']
# extract hour of day
time_info = train_df['created_at'].astype(str).str.split().str[1]
train_df['hour_of_day'] = time_info.str.split(":").str[0]
Let’s revisit our numeric features with missing data.
From the boxplots above, it seemed like most of our features tended to skew right. Thus, we’ll impute missing values for our numeric features with their median, as that is likely more representative of the center of their distributions compared to the mean.
values = {
'total_onshift_dashers': train_df['total_onshift_dashers'].median(),
'total_busy_dashers': train_df['total_busy_dashers'].median(),
'total_outstanding_orders': train_df['total_outstanding_orders'].median(),
'estimated_store_to_consumer_driving_duration': train_df['estimated_store_to_consumer_driving_duration'].median()
}
train_df[col].fillna(value=values, inplace=True)There are certainly other imputation strategies to consider here. Other approaches include KNN imputation (imputing missing values with the average of the K most “similar” observations), or building another regression model to predict those missing values from features thought to be potentially relevant. For now, we’ll proceed with median imputation for simplicity.
The last thing we’ll do before moving on to modeling is check correlations among our numeric features. Some of the regression algorithms we will experiment with assume that the features are independent i.e. no collinearity.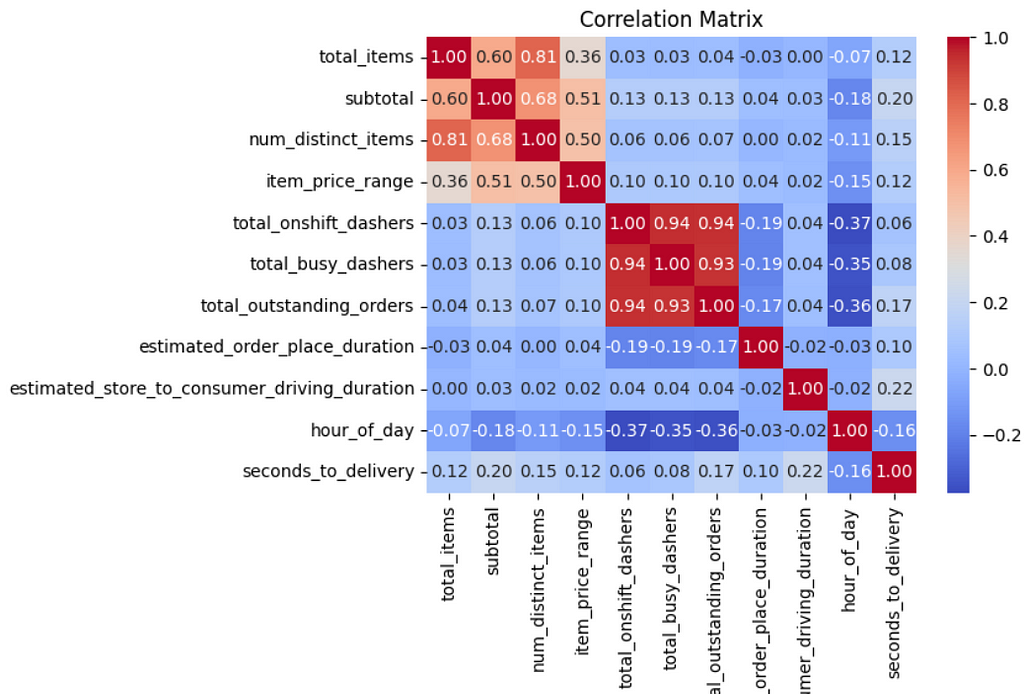
There is some high collinearity present:
- ‘total_items’ & ‘num_distinct_items’ (r > 0.8)
- ‘total_onshift_dashers’, ‘total_busy_dashers’, ‘total_outstanding_orders’ (r > 0.9)
Among sets of highly collinear features, we will only keep one from each set for the final feature set for the model. We will add this step as part of our preprocessing pipeline for our models.
Interestingly, each of our numeric features show fairly weak correlation (r < 0.2) with our prediction target (‘seconds_to_delivery’). This may give us a clue that a linear model will not effectively capture the relationship between our feature set & delivery duration (if there is any relationship).
Now that we’ve prepped & explored our data, let’s build some models.
Building Models
The first things to consider for modeling are what algorithms we want to build models with, and how to measure model performance.
We will experiment with the following regression algorithms, as they are algorithms commonly used for regression tasks. They include a mix of algorithms that can capture linear & non-linear relationships between the feature space & prediction target.
We’ll carry out hyperparameter tuning for each of the algorithms above to maximize the performance of each algorithm.
We’ll evaluate our models using Root Mean Squared Error (RMSE), as that will allow us to discuss the errors of each model in seconds, which makes sense in the context of delivery duration.
Although we prepped/cleaned our data, there are still some data transformations that need to be done to get the data compatible for each of the regression algorithms above. Specifically, the regression algorithms will require some or all of the following preprocessing steps prior to prediction:
- Imputing missing feature values
- Feature scaling (for Lasso & SVR only)
- Dropping highly correlated features
- One-hot encoding categorical features
These transformations may need to be applied to different subsets of our feature space, and some of these transformations may need to be applied in sequential order. Fortunately, we can use scikit-learn’s ColumnTransformer to specify which features to apply specific data transformations to, and scikit-learn’s Pipeline to define a series of data transformations to apply in sequence.
Note that we already took care of some of these preprocessing steps (such as imputing missing values) manually in our data preparation. However, defining this pipeline will come in handy when we want to apply this preprocessing workflow to new data, as these steps will already be saved as part of our model artifact.
Additionally, Lasso Regression & Support Vector Regression require features to be on consistent scales to maximize their effectiveness, since they perform distance-based computations. In contrast, Random Forest & Gradient Boosted Trees are built on top of Decision Trees, which involve threshold based splitting. Therefore, we’ll define two preprocessing pipelines, one with scaling and one without.
# sequence of transformations to apply to categorical features
categorical_pipeline = Pipeline(
steps=[
("categorical_imputer", SimpleImputer(strategy="constant", fill_value="unknown")),
("encoder", OneHotEncoder(handle_unknown="ignore", drop='first', sparse_output=False)),
]
)
# sequence of transformations to apply to numeric features
numeric_pipeline_scaled = Pipeline(
steps=[
("numeric_imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler()),
("drop_correlated_feats", DropHighlyCorrelatedFeatures()),
]
)
numeric_pipeline = Pipeline(
steps=[
("numeric_imputer", SimpleImputer(strategy="median")),
("drop_correlated_feats", DropHighlyCorrelatedFeatures()),
]
)
# combine numeric & categorical feature transformations into single ColumnTransformer() object
preprocessor_w_scaling = ColumnTransformer(
transformers=[
('numeric', numeric_pipeline_scaled, numeric_feats),
('cat', categorical_pipeline, categorical_feats),
],
)
preprocessor_wo_scaling = ColumnTransformer(
transformers=[
('numeric', numeric_pipeline, numeric_feats),
('cat', categorical_pipeline, categorical_feats),
]
)
Let’s build our first model using Lasso regression.
Lasso regression models a linear relationship between a scalar target and one or more explanatory variables. It includes a penalty term to the linear regression objective function that may zero out coefficients for features with little to no relationship with the prediction target.
Preprocessing requirements include:
- Feature scaling (fair regularization requires features to be on similar scales, and scaling may speed up the linear regression optimization process)
- One-hot encoding categorical features
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
# lasso regression preprocessing pipeline
lasso_reg = Pipeline(
steps=[
("preprocessor", preprocessor_w_scaling),
("regression", Lasso(random_state=13)),
]
)
# lasso regression hyperparameter space
lasso_param_grid = {
"regression__alpha": np.logspace(-3, -2, 10),
}
lasso_search_cv = GridSearchCV(lasso_reg, lasso_param_grid, scoring='neg_root_mean_squared_error', verbose=4)
# fit model, performing exhaustive search over hyperparameter space
lasso_search_cv.fit(df_X, df_y)
# retrieve results of hyperparameter tuning
lasso_cv_results_df = pd.DataFrame(lasso_search_cv.cv_results_)
lasso_cv_results_df.sort_values(by='mean_test_score', ascending=False).drop(columns=['params','split0_test_score','split1_test_score','split2_test_score','split3_test_score','split4_test_score'])
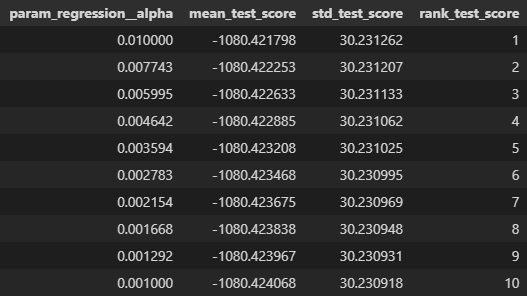
Lasso Regression Results:
- The best performing model had a root mean squared error of ~1080 seconds, or ~18 minutes. However, all models across different values of alpha had practically identical performance.
- On average, our predictions for delivery duration are ~18 minutes off from the true delivery duration. So, not super effective for predicting delivery duration.
Let’s move to Support Vector Regression, a popular regression algorithm derived from Support Vector Machines.
Preprocessing requirements include:
- Feature scaling (SVR computes dot products between observations in the feature space, so certain features may dominate the dot product computations if they are on widely different scales)
- One-hot encoding categorical features
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
svr_reg = Pipeline(
steps=[
("preprocessor", preprocessor_w_scaling),
("regression", SVR(kernel='poly', max_iter=1000)), # proceeding with polynomial kernel based on sub-par linear regression performance
]
)
svr_param_grid = {
"regression__C": np.logspace(-3, 1, 4),
'regression__epsilon': np.logspace(-3, 1, 4),
# 'regression__kernel': ['linear', 'poly', 'rbf']
}
svr_search_cv = GridSearchCV(svr_reg, svr_param_grid, verbose=4, scoring='neg_root_mean_squared_error')
svr_search_cv.fit(df_X, df_y)
svr_cv_results_df = pd.DataFrame(svr_search_cv.cv_results_)
svr_cv_results_df.sort_values("mean_test_score", ascending=False).drop(columns=['params','split0_test_score','split1_test_score','split2_test_score','split3_test_score','split4_test_score'])
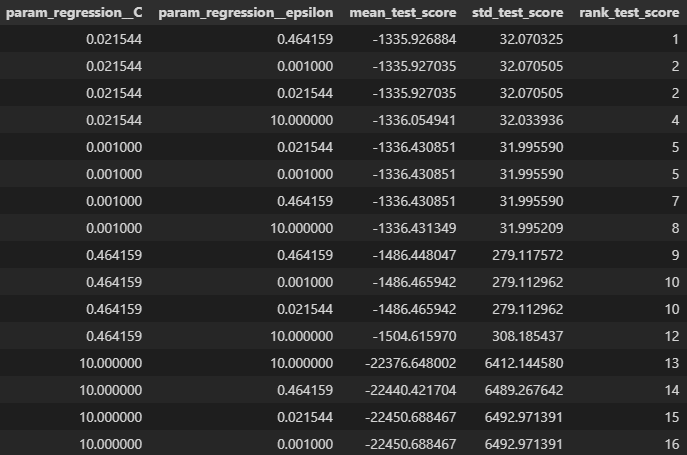
SVR results:
- Best performing model had a root mean squared error of ~1335 seconds (~22 minutes). These errors are ~4 minutes larger than our best Lasso Regression model.
Our next algorithm is Random Forest Regression.
Random Forest Regression is an ensemble learning method that combines the predictions of multiple decision trees, where each tree is built from a bootstrap sample drawn from the training set.
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
rfr_clf = Pipeline(
steps=[
("preprocessor", preprocessor_wo_scaling),
("regressor", RandomForestRegressor(random_state=13))
]
)
rfr_param_grid = {
"regressor__n_estimators": [10, 100, 200],
# 'regressor__max_depth': [None, 50],
'regressor__max_features': ['sqrt', 'log2', None],
}
rfr_search_cv = GridSearchCV(rfr_clf, rfr_param_grid, verbose=4, scoring='neg_root_mean_squared_error')
rfr_search_cv.fit(df_X, df_y)
rfr_cv_results = pd.DataFrame(rfr_search_cv.cv_results_)
rfr_cv_results = rfr_cv_results.sort_values("mean_test_score", ascending=False).drop(columns=['params','split0_test_score','split1_test_score','split2_test_score','split3_test_score','split4_test_score'])
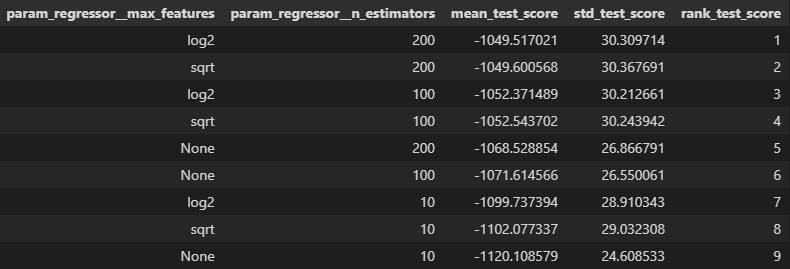
Random Forest results:
- Best performing model had a root mean squared error of ~1050 seconds (~17.5 minutes). So far, this is our best performing model, but not by much (errors are ~30 seconds lower than that of Lasso Regression).
Our last algorithm is Gradient Boosted Regression.
Gradient Boosted Regression is also an ensemble method like Random Forest Regression, but unlike the former, the learners in Gradient Boosted Regression are not independent — each base learner attempts to correct the errors of the previous.
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
gbr_clf = Pipeline(
steps=[
("preprocessor", preprocessor_wo_scaling),
("regressor", GradientBoostingRegressor(random_state=13))
]
)
gbr_param_grid = {
"regressor__n_estimators": [10, 100, 200],
'regressor__learning_rate': np.logspace(-3, 0, 4),
}
gbr_search_cv = GridSearchCV(gbr_clf, gbr_param_grid, verbose=4, scoring='neg_root_mean_squared_error')
gbr_search_cv.fit(df_X, df_y)
gbr_cv_results = pd.DataFrame(gbr_search_cv.cv_results_)
gbr_cv_results = gbr_cv_results.sort_values("mean_test_score", ascending=False).drop(columns=['params','split0_test_score','split1_test_score','split2_test_score','split3_test_score','split4_test_score'])
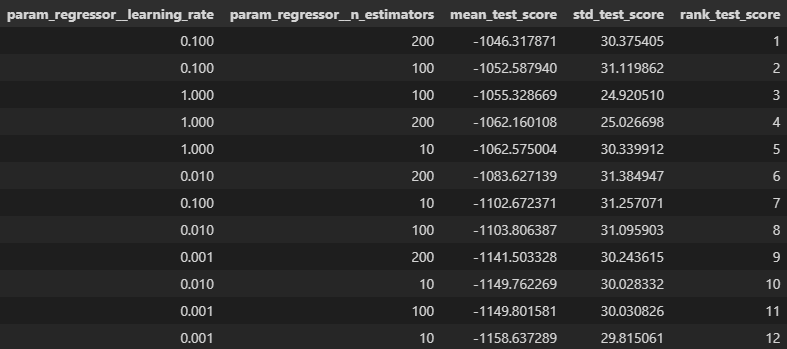
Gradient Boosted Regression results:
- Best performing model had a root mean squared error of ~1046 seconds (~17.5 minutes), which is practically identical to the performance we were getting from Random Forest Regression.
Let’s compare the RMSE scores from the best models we achieved with each regression algorithm.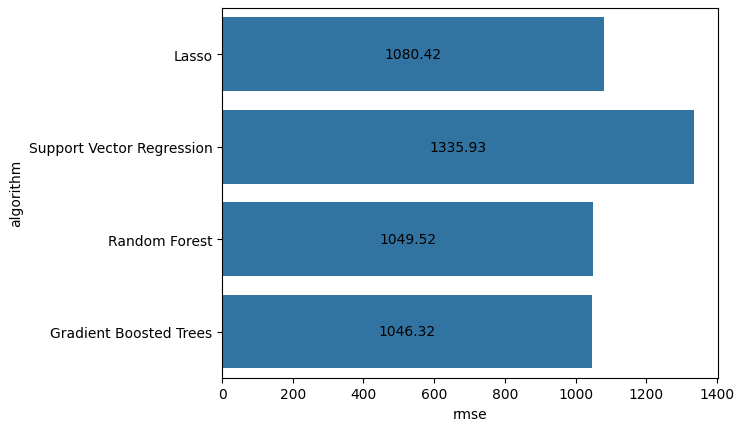
Our Gradient Boosted Regression model had the lowest RMSE, but outside of Support Vector Regression, all models had comparable performance. The RMSEs between Lasso, RFR, & GBR were all within 40 seconds of each other, and considering the prediction errors were already > 17 minutes off on average, this doesn’t seem like much.
That being said, we’ll proceed to evaluate our trained GBR model on the test set.
- From the weak correlations (r < 0.2) we saw between the features & delivery duration in our EDA, the nature of the relationship between the features & target is probably best captured in a non-linear fashion, so we’ll rule out Lasso for this reasoning.
- Between Gradient Boosting & Random Forests, we’ll choose Gradient Boosting for its potential to capture subtle, complex relationships due to its goal towards reducing bias. When model performance is this close, other factors to consider could include interpretability, robustess to outliers, and reliance on hyperparameter tuning.
We’ll write out the hyperparameter-tuned GBR model artifact. This model serialization will contain the necessary data transformations prior to prediction, as well as the model hyperparameters that led to optimal GBR performance.
# Use joblib for efficient model serialization
import joblib
# Save trained GBR model
joblib.dump(gbr_search_cv.best_estimator_, '../models/best_model.pkl')
print("Best model saved to 'best_model.pkl'")
Final Model Evaluation
Now, we’ll evaluate our chosen model on our holdout test data. Before we generate predictions on the test data, we’ll have to repeat some feature engineering steps that we did in our initial data prep. Specifically, we’ll need to create the following features in our test data:
- ‘store_id_freq’
- ‘store_category_type’
- ‘item_price_range’
- ‘hour_of_day’
The rest of the data cleaning/preprocessing steps (imputing missing values, feature scaling, dropping correlated features) will be taken care of in the pipeline defined in the model artifact.
from feature_eng_utils import encode_frequency, map_to_category_type
# create store_id_freq
value_counts = test_df['store_id'].value_counts()
percentiles = np.percentile(value_counts, [50, 75, 90, 99])
test_df['store_id_freq'] = test_df['store_id'].apply(lambda x: encode_frequency(value_counts[x], percentiles))
# create store_category_type
test_df['store_category_type'] = test_df['store_primary_category'].apply(lambda x: map_to_category_type(x))
# create item_price_range
test_df['item_price_range'] = test_df['max_item_price'] - test_df['min_item_price']
# create hour_of_day
time_info = test_df['created_at'].astype(str).str.split().str[1]
test_df['hour_of_day'] = time_info.str.split(":").str[0]
Let’s evaluate our model on the test data.
import joblib
from custom_transformers import DropHighlyCorrelatedFeatures
from sklearn.metrics import root_mean_squared_error
# Load the saved model
loaded_model = joblib.load('../models/best_model.pkl')
# Make predictions
y_pred = loaded_model.predict(test_df_X)
# Compute root mean squared error
test_rmse = root_mean_squared_error(test_df_y, y_pred)
print("Test RMSE:", test_rmse)
Our final test RMSE comes out to be ~1080 seconds.
Thus, on average, our predictions for delivery duration are ~18 minutes off from the true delivery duration. So overall, pretty bad. I’m not sure if DoorDash models delivery duration from these features only, but I certainly would not recommend using this model as an endpoint for returning delivery duration estimates.
Some ideas for further work/investigation could include the following:
- Investigating important features that came up during prediction & look to gather more data related to those identified features.
- Some of the original features were ID values without any context (‘market_id’, ‘order_protocol’). Retrieving more info on what those features mean may be helpful to improve some of the feature engineering decisions we made.
- Our approach for imputing missing values was fairly basic. Additional investigation could be done to determine whether there was any pattern in those missing values. If so, our imputing approach may have been inappropriate.
Conclusion
If you made it this far, thanks! There were a lot of data investigation & modeling decisions that we went through, many of which had no clear cut answer. However, I did my best to lay out all the relevant decisions made during the investigation process, as well as the reasoning behind those decisions. If there’s any part of the process that you would’ve done differently, please let me know in the comments, I’d love to hear it!
I read through many great resources while doing this investigation. I did my best to include most of them below — I highly recommend checking at least some of them out!
Sources
Missing data:
Handling high cardinality features:
Pipelines & Data Transformers:
- https://scikit-learn.org/1.6/data_transforms.html
- https://scikit-learn.org/stable/auto_examples/compose/index.html
Scikit-learn Regression APIs:
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LassoCV.html
- https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html
- https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
- https://scikit-learn.org/1.5/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html
Hyperparameter tuning:
- https://scikit-learn.org/1.6/modules/grid_search.html#
- https://www.kaggle.com/code/kenjee/exhaustive-regression-parameter-tuning#ML-Algorithms---Regression-Example
- https://www.reddit.com/r/datascience/comments/mwl2zj/do_you_often_find_hyperparam_tuning_does_very/
- https://www.linkedin.com/advice/3/when-should-you-stop-tuning-your-hyperparameters-8j9pf
Model selection:
Most of all, the entirety of the scikit-learn user guide & examples.
The author has created all the images in this article.
Building a Regression Model: Delivery Duration Prediction was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.


 Editor-Admin
Editor-Admin 





