Does It Matter That Online Experiments Interact?

What interactions do, why they are just like any other change in the environment post-experiment, and some reassurance

Experiments do not run one at a time. At any moment, hundreds to thousands of experiments run on a mature website. The question comes up: what if these experiments interact with each other? Is that a problem? As with many interesting questions, the answer is “yes and no.” Read on to get even more definite, actionable, entirely clear, and confident takes like that!

Definitions: Experiments interact when the treatment effect for one experiment depends on which variant of another experiment the unit gets assigned to.

For example, suppose we have an experiment testing a new search model and another testing a new recommendation model, powering a “people also bought” module. Both experiments are ultimately about helping customers find what they want to buy. Units assigned to the better recommendation algorithm may have a smaller treatment effect in the search experiment because they are less likely to be influenced by the search algorithm: they made their purchase because of the better recommendation.

Some empirical evidence suggests that typical interaction effects are small. Maybe you don’t find this particularly comforting. I’m not sure I do, either. After all, the size of interaction effects depends on the experiments we run. For your particular organization, experiments might interact more or less. It might be the case that interaction effects are larger in your context than at the companies typically profiled in these types of analyses.

So, this blog post is not an empirical argument. It’s theoretical. That means it includes math. So it goes. We will try to understand the issues with interactions with an explicit model without reference to a particular company’s data. Even if interaction effects are relatively large, we’ll find that they rarely matter for decision-making. Interaction effects must be massive and have a peculiar pattern to affect which experiment wins. The point of the blog is to bring you peace of mind.

Interactions Aren’t So Special, And They Aren’t So Bad

Suppose we have two A/B experiments. Let Z = 1 indicate treatment in the first experiment and W = 1 indicate treatment in the second experiment. Y is the metric of interest.

The treatment effect in experiment 1 is: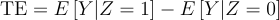

Let’s decompose these terms to look at how interaction impacts the treatment effect.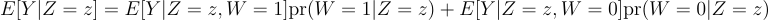

Bucketing for one randomized experiment is independent of bucketing in another randomized experiment, so: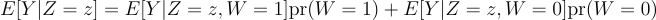

So, the treatment effect is: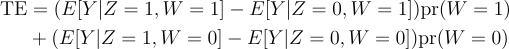

Or, more succinctly, the treatment effect is the weighted average of the treatment effect within the W=1 and W=0 populations: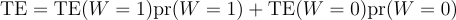

One of the great things about just writing the math down is that it makes our problem concrete. We can see exactly the form the bias from interaction will take and what will determine its size.

The problem is this: only W = 1 or W = 0 will launch after the second experiment ends. So, the environment during the first experiment will not be the same as the environment after it. This introduces the following bias in the treatment effect:

Suppose W = w launches, then the post-experiment treatment effect for the first experiment, TE(W=w), is mismeasured by the experiment treatment effect, TE, leading to the bias: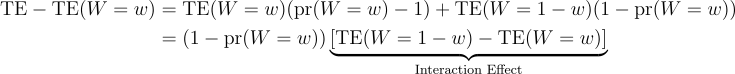

If there is an interaction between the second experiment and the first, then TE(W=1-w) — TE(W=w) != 0, so there is a bias.

So, yes, interactions cause a bias. The bias is directly proportional to the size of the interaction effect.

But interactions are not special. Anything that differs between the experiment’s environment and the future environment that affects the treatment effect leads to a bias with the same form. Does your product have seasonal demand? Was there a large supply shock? Did inflation rise sharply? What about the butterflies in Korea? Did they flap their wings?

Online Experiments are not Laboratory Experiments. We cannot control the environment. The economy is not under our control (sadly). We always face biases like this.

So, Online Experiments are not about estimating treatment effects that hold in perpetuity. They are about making decisions. Is A better than B? That answer is unlikely to change because of an interaction effect for the same reason that we don’t usually worry about it flipping because we ran the experiment in March instead of some other month of the year.

For interactions to matter for decision-making, we need, say, TE ≥ 0 (so we would launch B in the first experiment) and TE(W=w) < 0 (but we should have launched A given what happened in the second experiment).

TE ≥ 0 if and only if: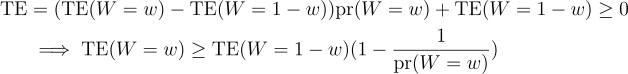

Taking the typical allocation pr(W=w) = 0.50, this means: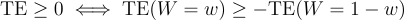

Because TE(W=w) < 0, this can only be true if TE(W=1-w) > 0. Which makes sense. For interactions to be a problem for decision-making, the interaction effect has to be large enough that an experiment that is negative under one treatment is positive under the other.

The interaction effect has to be extreme at typical 50–50 allocations. If the treatment effect is +$2 per unit under one treatment, the treatment must be less than -$2 per unit under the other for interactions to affect decision-making. To make the wrong decision from the standard treatment effect, we’d have to be cursed with massive interaction effects that change the sign of the treatment and maintain the same magnitude!

This is why we’re not concerned about interactions and all those other factors (seasonality, etc.) that we can’t keep the same during and after the experiment. The change in environment would have to radically alter the user’s experience of the feature. It probably doesn’t.

It’s always a good sign when your final take includes “probably.”

Thanks for reading!

Zach

Connect at: https://linkedin.com/in/zlflynn

Does It Matter That Online Experiments Interact? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.