Modeling DAU with Markov Chain
How to predict DAU using Duolingo’s growth model and control the prediction1. IntroductionDoubtlessly, DAU, WAU, and MAU — daily, weekly, and monthly active users — are critical business metrics. An article “How Duolingo reignited user growth” by Jorge Mazal, former CPO of Duolingo, is #1 in the Growth section of Lenny’s Newsletter blog. In this article, Jorge paid special attention to the methodology Duolingo used to model the DAU metric (see another article “Meaningful metrics: how data sharpened the focus of product teams” by Erin Gustafson). This methodology has multiple strengths, but I’d like to focus on how one can use this approach for DAU forecasting.The new year is coming soon, so many companies are planning their budgets for the next year these days. Cost estimations often require DAU forecasts. In this article, I’ll show how you can get this prediction using Duolingo’s growth model. I’ll explain why this approach is better compared to standard time-series forecasting methods and how you can adjust the prediction according to your teams’ plans (e.g., marketing, activation, product teams).The article text goes along with the code, and a simulated dataset is attached so the research is fully reproducible. The Jupyter notebook version is available here. In the end, I’ll share a DAU “calculator” designed in Google Spreadsheet format.I’ll be narrating on behalf of the collective “we” as if we’re talking together.2. MethodologyA quick recap on how the Duolingo’s growth model works. At day d (d = 1, 2, … ) of a user’s lifetime, the user can be in one of the following 7 (mutually-exclusive) states: new, current, reactivated, resurrected, at_risk_wau, at_risk_mau, dormant. The states are defined according to indicators of whether a user was active today, in the last 7 days, or in the last 30 days. The definition summary is given in the table below:Having these states defined (as a set S), we can consider user behavior as a Markov chain. Here’s an example of a user’s trajectory: new→ current→ current→ at_risk_wau→...→ at_risk_mau→...→ dormant. Let M be a transition matrix associated with this Markov process: m_{i, j} = P(s_j | s_i) are the probabilities that a user moves to state s_j right after being at state s_i, where s_i, s_j ∈ S. Such a matrix is inferred from the historical data.If we assume that user behavior is stationary (independent of time), the matrix M fully describes the states of all users in the future. Suppose that the vector u_0 of length 7 contains the counts of users in certain states on a given day, denoted as day 0. According to the Markov model, on the next day 1, we expect to have the following number of users states u_1:Applying this formula recursively, we derive the number of users in certain states on any arbitrary day t > 0 in the future.Besides the initial distribution u_0, we need to provide the number of new users that will appear in the product each day in the future. We’ll address this problem as a general time-series forecasting.Now, having u_t calculated, we can determine DAU values on day t:DAU_t = #New_t + #Current_t + #Reactivated_t + #Resurrected_tAdditionally, we can easily calculate WAU and MAU metrics:WAU_t = DAU_t + #AtRiskWau_t,MAU_t = DAU_t + #AtRiskWau_t + #AtRiskMau_t.Finally, here’s the algorithm outline:For each prediction day t = 1, …, T, calculate the expected number of new users #New_1, …, #New_T.For each lifetime day of each user, assign one of the 7 states.Calculate the transition matrix M from the historical data.Calculate initial state counts u_0 corresponding to day t=0.Recursively calculate u_{t+1} = M^T * u_t.Calculate DAU, WAU, and MAU for each prediction day t = 1, …, T.3. ImplementationThis section is devoted to technical aspects of the implementation. If you’re interested in studying the model properties rather than code, you may skip this section and go to the Section 4.3.1 DatasetWe use a simulated dataset based on historical data of a SaaS app. The data is stored in the dau_data.csv.gz file and contains three columns: user_id, date, and registration_date. Each record indicates a day when a user was active. The dataset includes activity indicators for 51480 users from 2020-11-01 to 2023-10-31. Additionally, data from October 2020 is included to calculate user states properly, as the at_risk_mau and dormant states require data from one month prior.import pandas as pddf = pd.read_csv('dau_data.csv.gz', compression='gzip')df['date'] = pd.to_datetime(df['date'])df['registration_date'] = pd.to_datetime(df['registration_date'])print(f'Shape: {df.shape}')print(f'Total users: {df['user_id'].nunique()}')print(f'Data range: [{df['date'].min()}, {df['date'].max()}]')df.head()Shape: (667236, 3)Total users: 51480Data range: [2020-10-01 00:00:00, 2023-10-31 00:00:00]This is how the DAU time-series looks like.df.groupby('date').size()\ .plot(title='DAU, historical')Suppose that today is 2023–10–31 and we want to predict the DAU metric for the next 2024
How to predict DAU using Duolingo’s growth model and control the prediction
1. Introduction
Doubtlessly, DAU, WAU, and MAU — daily, weekly, and monthly active users — are critical business metrics. An article “How Duolingo reignited user growth” by Jorge Mazal, former CPO of Duolingo, is #1 in the Growth section of Lenny’s Newsletter blog. In this article, Jorge paid special attention to the methodology Duolingo used to model the DAU metric (see another article “Meaningful metrics: how data sharpened the focus of product teams” by Erin Gustafson). This methodology has multiple strengths, but I’d like to focus on how one can use this approach for DAU forecasting.
The new year is coming soon, so many companies are planning their budgets for the next year these days. Cost estimations often require DAU forecasts. In this article, I’ll show how you can get this prediction using Duolingo’s growth model. I’ll explain why this approach is better compared to standard time-series forecasting methods and how you can adjust the prediction according to your teams’ plans (e.g., marketing, activation, product teams).
The article text goes along with the code, and a simulated dataset is attached so the research is fully reproducible. The Jupyter notebook version is available here. In the end, I’ll share a DAU “calculator” designed in Google Spreadsheet format.
I’ll be narrating on behalf of the collective “we” as if we’re talking together.
2. Methodology
A quick recap on how the Duolingo’s growth model works. At day d (d = 1, 2, … ) of a user’s lifetime, the user can be in one of the following 7 (mutually-exclusive) states: new, current, reactivated, resurrected, at_risk_wau, at_risk_mau, dormant. The states are defined according to indicators of whether a user was active today, in the last 7 days, or in the last 30 days. The definition summary is given in the table below: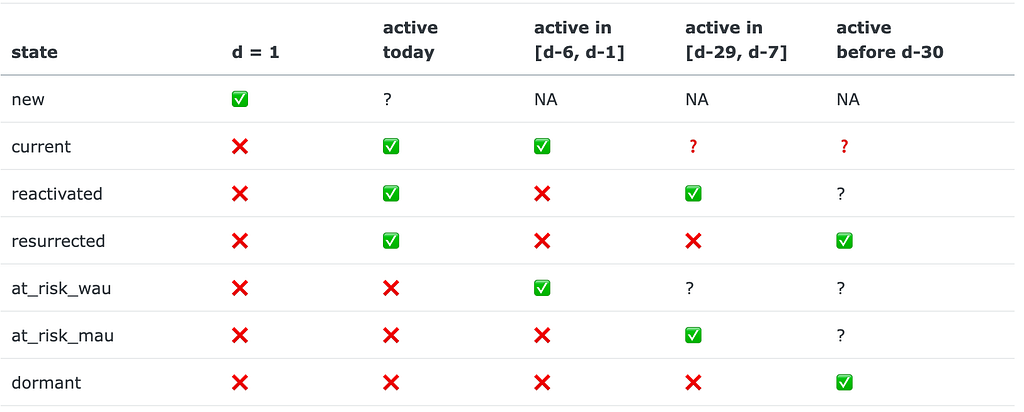
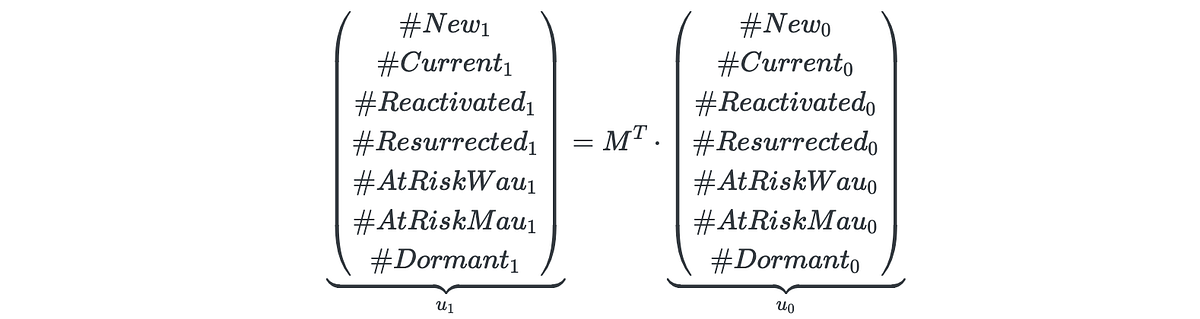
Having these states defined (as a set S), we can consider user behavior as a Markov chain. Here’s an example of a user’s trajectory: new→ current→ current→ at_risk_wau→...→ at_risk_mau→...→ dormant. Let M be a transition matrix associated with this Markov process: m_{i, j} = P(s_j | s_i) are the probabilities that a user moves to state s_j right after being at state s_i, where s_i, s_j ∈ S. Such a matrix is inferred from the historical data.
If we assume that user behavior is stationary (independent of time), the matrix M fully describes the states of all users in the future. Suppose that the vector u_0 of length 7 contains the counts of users in certain states on a given day, denoted as day 0. According to the Markov model, on the next day 1, we expect to have the following number of users states u_1:
Applying this formula recursively, we derive the number of users in certain states on any arbitrary day t > 0 in the future.
Besides the initial distribution u_0, we need to provide the number of new users that will appear in the product each day in the future. We’ll address this problem as a general time-series forecasting.
Now, having u_t calculated, we can determine DAU values on day t:
DAU_t = #New_t + #Current_t + #Reactivated_t + #Resurrected_t
Additionally, we can easily calculate WAU and MAU metrics:
WAU_t = DAU_t + #AtRiskWau_t,
MAU_t = DAU_t + #AtRiskWau_t + #AtRiskMau_t.
Finally, here’s the algorithm outline:
- For each prediction day t = 1, …, T, calculate the expected number of new users #New_1, …, #New_T.
- For each lifetime day of each user, assign one of the 7 states.
- Calculate the transition matrix M from the historical data.
- Calculate initial state counts u_0 corresponding to day t=0.
- Recursively calculate u_{t+1} = M^T * u_t.
- Calculate DAU, WAU, and MAU for each prediction day t = 1, …, T.
3. Implementation
This section is devoted to technical aspects of the implementation. If you’re interested in studying the model properties rather than code, you may skip this section and go to the Section 4.
3.1 Dataset
We use a simulated dataset based on historical data of a SaaS app. The data is stored in the dau_data.csv.gz file and contains three columns: user_id, date, and registration_date. Each record indicates a day when a user was active. The dataset includes activity indicators for 51480 users from 2020-11-01 to 2023-10-31. Additionally, data from October 2020 is included to calculate user states properly, as the at_risk_mau and dormant states require data from one month prior.
import pandas as pd
df = pd.read_csv('dau_data.csv.gz', compression='gzip')
df['date'] = pd.to_datetime(df['date'])
df['registration_date'] = pd.to_datetime(df['registration_date'])
print(f'Shape: {df.shape}')
print(f'Total users: {df['user_id'].nunique()}')
print(f'Data range: [{df['date'].min()}, {df['date'].max()}]')
df.head()
Shape: (667236, 3)
Total users: 51480
Data range: [2020-10-01 00:00:00, 2023-10-31 00:00:00]
This is how the DAU time-series looks like.
df.groupby('date').size()\
.plot(title='DAU, historical')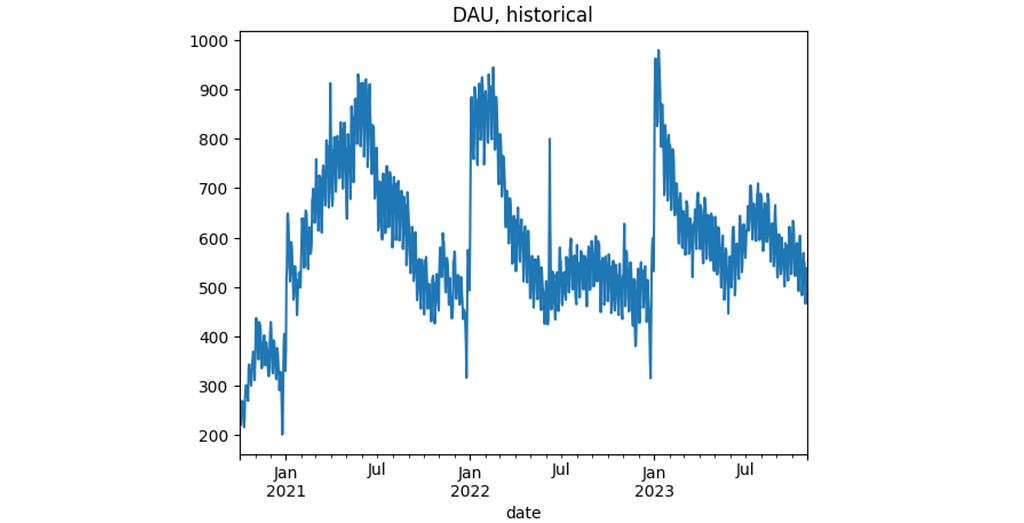
Suppose that today is 2023–10–31 and we want to predict the DAU metric for the next 2024 year. We define a couple of global constants PREDICTION_START and PREDICTION_END which encompass the prediction period.
PREDICTION_START = '2023-11-01'
PREDICTION_END = '2024-12-31'
3.2 Predicting new users amount
Let’s start from the new users prediction. We use the prophet library as one of the easiest ways to forecast time-series data. The new_users Series contains such data. We extract it from the original df dataset selecting the rows where the registration date is equal to the date.
new_users = df[df['date'] == df['registration_date']]\
.groupby('date').size()
new_users.head()
date
2020-10-01 4
2020-10-02 4
2020-10-03 3
2020-10-04 4
2020-10-05 8
dtype: int64
prophet requires a time-series as a DataFrame containing two columns ds and y, so we reformat the new_users Series to the new_users_prophet DataFrame. Another thing we need to prepare is to create the future variable containing certain days for prediction: from prediction_start to prediction_end. This logic is implemented in the predict_new_users function. The plot below illustrates predictions for both past and future periods.
import logging
import matplotlib.pyplot as plt
from prophet import Prophet
# suppress prophet logs
logging.getLogger('prophet').setLevel(logging.WARNING)
logging.getLogger('cmdstanpy').disabled=True
def predict_new_users(prediction_start, prediction_end, new_users_train, show_plot=True):
"""
Forecasts a time-seires for new users
Parameters
----------
prediction_start : str
Date in YYYY-MM-DD format.
prediction_end : str
Date in YYYY-MM-DD format.
new_users_train : pandas.Series
Historical data for the time-series preceding the prediction period.
show_plot : boolean, default=True
If True, a chart with the train and predicted time-series values is displayed.
Returns
-------
pandas.Series
Series containing the predicted values.
"""
m = Prophet()
new_users_train = new_users_train\
.loc[new_users_train.index < prediction_start]
new_users_prophet = pd.DataFrame({
'ds': new_users_train.index,
'y': new_users_train.values
})
m.fit(new_users_prophet)
periods = len(pd.date_range(prediction_start, prediction_end))
future = m.make_future_dataframe(periods=periods)
new_users_pred = m.predict(future)
if show_plot:
m.plot(new_users_pred)
plt.title('New users prediction');
new_users_pred = new_users_pred\
.assign(yhat=lambda _df: _df['yhat'].astype(int))\
.rename(columns={'ds': 'date', 'yhat': 'count'})\
.set_index('date')\
.clip(lower=0)\
['count']
return new_users_pred
new_users_pred = predict_new_users(PREDICTION_START, PREDICTION_END, new_users)
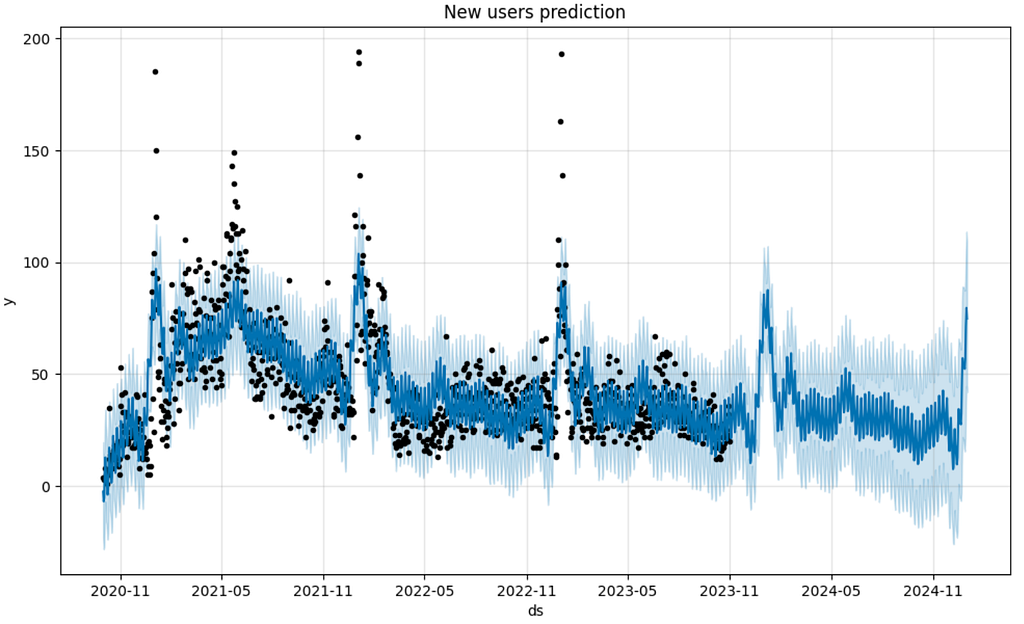
The new_users_pred Series stores the predicted users amount.
new_users_pred.tail(5)
date
2024-12-27 52
2024-12-28 56
2024-12-29 71
2024-12-30 79
2024-12-31 74
Name: count, dtype: int64
3.3 Getting the states
In practice, the most calculations are reasonable to execute as SQL queries to a database where the data is stored. Hereafter, we will simulate such querying using the duckdb library.
We want to assign one of the 7 states to each day of a user’s lifetime within the app. According to the definition, for each day, we need to consider at least the past 30 days. This is where SQL window functions come in. However, since the df data contains only records of active days, we need to explicitly extend them and include the days when a user was not active. In other words, instead of this list of records:
user_id date registration_date
1234567 2023-01-01 2023-01-01
1234567 2023-01-03 2023-01-01
we’d like to get a list like this:
user_id date is_active registration_date
1234567 2023-01-01 TRUE 2023-01-01
1234567 2023-01-02 FALSE 2023-01-01
1234567 2023-01-03 TRUE 2023-01-01
1234567 2023-01-04 FALSE 2023-01-01
1234567 2023-01-05 FALSE 2023-01-01
... ... ... ...
1234567 2023-10-31 FALSE 2023-01-01
For readability purposes we split the following SQL query into multiple subqueries.
- full_range: Create a full sequence of dates for each user.
- dau_full: Get the full list of both active and inactive records.
- states: Assign one of the 7 states for each day of a user's lifetime.
import duckdb
DATASET_START = '2020-11-01'
DATASET_END = '2023-10-31'
OBSERVATION_START = '2020-10-01'
query = f"""
WITH
full_range AS (
SELECT
user_id, UNNEST(generate_series(greatest(registration_date, '{OBSERVATION_START}'), date '{DATASET_END}', INTERVAL 1 DAY))::date AS date
FROM (
SELECT DISTINCT user_id, registration_date FROM df
)
),
dau_full AS (
SELECT
fr.user_id,
fr.date,
df.date IS NOT NULL AS is_active,
registration_date
FROM full_range AS fr
LEFT JOIN df USING(user_id, date)
),
states AS (
SELECT
user_id,
date,
is_active,
first_value(registration_date IGNORE NULLS) OVER (PARTITION BY user_id ORDER BY date) AS registration_date,
SUM(is_active::int) OVER (PARTITION BY user_id ORDER BY date ROWS BETWEEN 6 PRECEDING and 1 PRECEDING) AS active_days_back_6d,
SUM(is_active::int) OVER (PARTITION BY user_id ORDER BY date ROWS BETWEEN 29 PRECEDING and 1 PRECEDING) AS active_days_back_29d,
CASE
WHEN date = registration_date THEN 'new'
WHEN is_active = TRUE AND active_days_back_6d BETWEEN 1 and 6 THEN 'current'
WHEN is_active = TRUE AND active_days_back_6d = 0 AND IFNULL(active_days_back_29d, 0) > 0 THEN 'reactivated'
WHEN is_active = TRUE AND active_days_back_6d = 0 AND IFNULL(active_days_back_29d, 0) = 0 THEN 'resurrected'
WHEN is_active = FALSE AND active_days_back_6d > 0 THEN 'at_risk_wau'
WHEN is_active = FALSE AND active_days_back_6d = 0 AND ifnull(active_days_back_29d, 0) > 0 THEN 'at_risk_mau'
ELSE 'dormant'
END AS state
FROM dau_full
)
SELECT user_id, date, state FROM states
WHERE date BETWEEN '{DATASET_START}' AND '{DATASET_END}'
ORDER BY user_id, date
"""
states = duckdb.sql(query).df()
The query results are kept in the states DataFrame: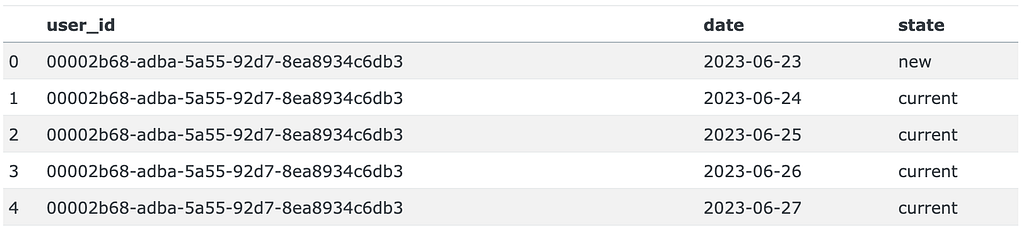
3.4 Calculating the transition matrix
Having obtained these states, we can calculate state transition frequencies. In the Section 4.3 we’ll study how the prediction depends on a period in which transitions are considered, so it’s reasonable to pre-aggregate this data on daily basis. The resulting transitions DataFrame contains date, state_from, state_to, and cnt columns.
Now, we can calculate the transition matrix M. We implement the get_transition_matrix function, which accepts the transitions DataFrame and a pair of dates that encompass the transitions period to be considered.
As a baseline, let’s calculate the transition matrix for the whole year from 2022-11-01 to 2023-10-31.
M = get_transition_matrix(transitions, '2022-11-01', '2023-10-31')
M
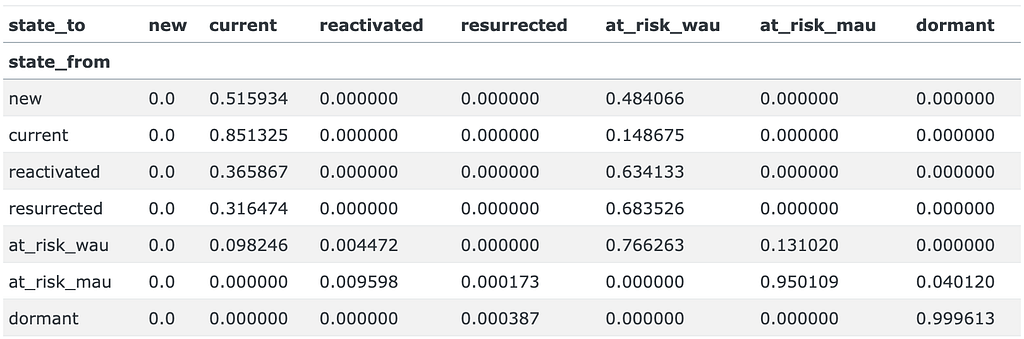
The sum of each row of any transition matrix equals 1 since it represents the probabilities of moving from one state to any other state.
3.5 Getting the initial state counts
An initial state is retrieved from the states DataFrame by the get_state0 function and the corresponding SQL query. The only argument of the function is the date for which we want to get the initial state. We assign the result to the state0 variable.
def get_state0(date):
query = f"""
SELECT state, count(*) AS cnt
FROM states
WHERE date = '{date}'
GROUP BY state
"""
state0 = duckdb.sql(query).df()
state0 = state0.set_index('state').reindex(states_order)['cnt']
return state0
state0 = get_state0(DATASET_END)
state0
state
new 20
current 475
reactivated 15
resurrected 19
at_risk_wau 404
at_risk_mau 1024
dormant 49523
Name: cnt, dtype: int64
3.6 Predicting DAU
The predict_dau function below accepts all the previous variables required for the DAU prediction and makes this prediction for a date range defined by the start_date and end_date arguments.
def predict_dau(M, state0, start_date, end_date, new_users):
"""
Predicts DAU over a given date range.
Parameters
----------
M : pandas.DataFrame
Transition matrix representing user state changes.
state0 : pandas.Series
counts of initial state of users.
start_date : str
Start date of the prediction period in 'YYYY-MM-DD' format.
end_date : str
End date of the prediction period in 'YYYY-MM-DD' format.
new_users : int or pandas.Series
The expected amount of new users for each day between `start_date` and `end_date`.
If a Series, it should have dates as the index.
If an int, the same number is used for each day.
Returns
-------
pandas.DataFrame
DataFrame containing the predicted DAU, WAU, and MAU for each day in the date range,
with columns for different user states and tot.
"""
dates = pd.date_range(start_date, end_date)
dates.name = 'date'
dau_pred = []
new_dau = state0.copy()
for date in dates:
new_dau = (M.transpose() @ new_dau).astype(int)
if isinstance(new_users, int):
new_users_today = new_users
else:
new_users_today = new_users.astype(int).loc[date]
new_dau.loc['new'] = new_users_today
dau_pred.append(new_dau.tolist())
dau_pred = pd.DataFrame(dau_pred, index=dates, columns=states_order)
dau_pred['dau'] = dau_pred['new'] + dau_pred['current'] + dau_pred['reactivated'] + dau_pred['resurrected']
dau_pred['wau'] = dau_pred['dau'] + dau_pred['at_risk_wau']
dau_pred['mau'] = dau_pred['dau'] + dau_pred['at_risk_wau'] + dau_pred['at_risk_mau']
return dau_pred
dau_pred = predict_dau(M, state0, PREDICTION_START, PREDICTION_END, new_users_pred)
dau_pred
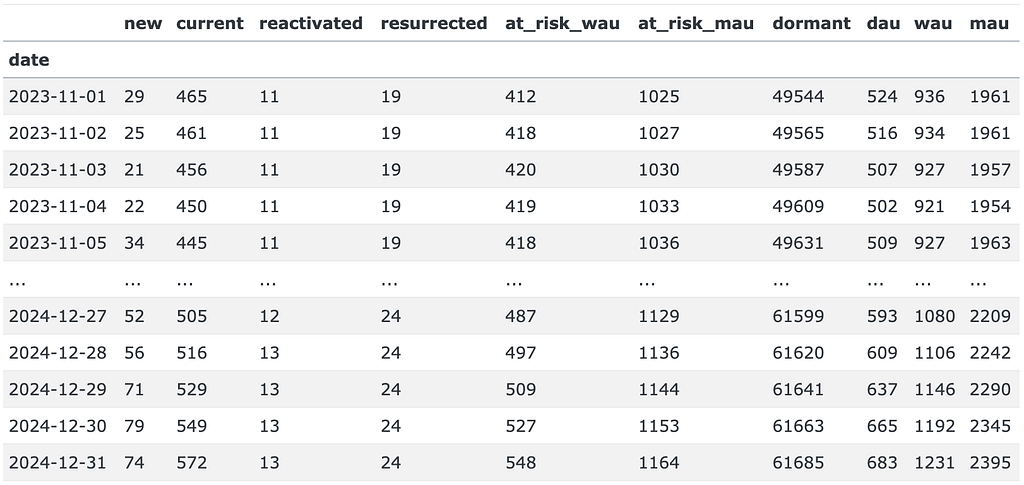
This is how the DAU prediction dau_pred looks like for the PREDICTION_START - PREDICTION_END period. Besides the expected dau, wau, and mau columns, the output contains the number of users in each state for each prediction date.
Finally, we calculate the ground-truth values of DAU, WAU, and MAU (along with the user state counts), keep them in the dau_true DataFrame, and plot the predicted and true values altogether.
query = f"""
SELECT date, state, COUNT(*) AS cnt
FROM states
GROUP BY date, state
ORDER BY date, state;
"""
dau_true = duckdb.sql(query).df()
dau_true['date'] = pd.to_datetime(dau_true['date'])
dau_true = dau_true.pivot(index='date', columns='state', values='cnt')
dau_true['dau'] = dau_true['new'] + dau_true['current'] + dau_true['reactivated'] + dau_true['resurrected']
dau_true['wau'] = dau_true['dau'] + dau_true['at_risk_wau']
dau_true['mau'] = dau_true['dau'] + dau_true['at_risk_wau'] + dau_true['at_risk_mau']
dau_true.head()
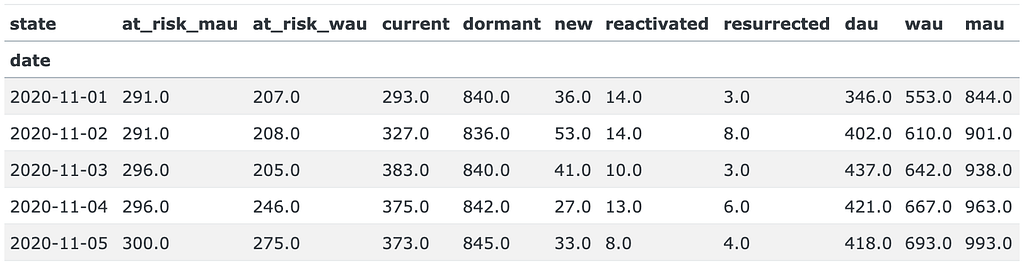
pd.concat([dau_true['dau'], dau_pred['dau']])\
.plot(title='DAU, historical & predicted');
plt.axvline(PREDICTION_START, color='k', linestyle='--');
We’ve obtained the prediction but so far it’s not clear whether it’s fair or not. In the next section, we’ll evaluate the model.
4. Model evaluation
4.1 Baseline model
First of all, let’s check whether we really need to build a complex model to predict DAU. Wouldn’t it be better to predict DAU as a general time-series using the mentioned prophet library? The function predict_dau_prophet below implements this. We try to use some tweaks available in the library in order to make the prediction more accurate. In particular:
- we use logistic model instead of linear to avoid negative values;
- we add explicitly monthly and yearly seasonality;
- we remove the outliers;
- we explicitly define a peak period in January and February as “holidays”.
def predict_dau_prophet(prediction_start, prediction_end, dau_true, show_plot=True):
# assigning peak days for the new year
holidays = pd.DataFrame({
'holiday': 'january_spike',
'ds': pd.date_range('2022-01-01', '2022-01-31', freq='D').tolist() + \
pd.date_range('2023-01-01', '2023-01-31', freq='D').tolist(),
'lower_window': 0,
'upper_window': 40
})
m = Prophet(growth='logistic', holidays=holidays)
m.add_seasonality(name='monthly', period=30.5, fourier_order=3)
m.add_seasonality(name='yearly', period=365, fourier_order=3)
train = dau_true.loc[(dau_true.index < prediction_start) & (dau_true.index >= '2021-08-01')]
train_prophet = pd.DataFrame({'ds': train.index, 'y': train.values})
# removining outliers
train_prophet.loc[train_prophet['ds'].between('2022-06-07', '2022-06-09'), 'y'] = None
train_prophet['new_year_peak'] = (train_prophet['ds'] >= '2022-01-01') &\
(train_prophet['ds'] <= '2022-02-14')
m.add_regressor('new_year_peak')
# setting logistic upper and lower bounds
train_prophet['cap'] = dau_true.max() * 1.1
train_prophet['floor'] = 0
m.fit(train_prophet)
periods = len(pd.date_range(prediction_start, prediction_end))
future = m.make_future_dataframe(periods=periods)
future['new_year_peak'] = (future['ds'] >= '2022-01-01') & (future['ds'] <= '2022-02-14')
future['cap'] = dau_true.max() * 1.1
future['floor'] = 0
pred = m.predict(future)
if show_plot:
m.plot(pred);
# converting the predictions to an appropriate format
pred = pred\
.assign(yhat=lambda _df: _df['yhat'].astype(int))\
.rename(columns={'ds': 'date', 'yhat': 'count'})\
.set_index('date')\
.clip(lower=0)\
['count']\
.loc[lambda s: (s.index >= prediction_start) & (s.index <= prediction_end)]
return pred
The fact that the code turns out to be quite sophisticated indicates that one can’t simply apply prophet to the DAU time-series.
Hereafter we test a prediction for multiple predicting horizons: 3, 6, and 12 months. As a result, we get 3 test sets:
- 3-months horizon: 2023-08-01 - 2023-10-31,
- 6-months horizon: 2023-05-01 - 2023-10-31,
- 1-year horizon: 2022-11-01 - 2023-10-31.
For each test set we calculate the MAPE loss function.
from sklearn.metrics import mean_absolute_percentage_error
mapes = []
prediction_end = '2023-10-31'
prediction_horizon = [3, 6, 12]
for offset in prediction_horizon:
prediction_start = pd.to_datetime(prediction_end) - pd.DateOffset(months=offset - 1)
prediction_start = prediction_start.replace(day=1)
prediction_end = '2023-10-31'
pred = predict_dau_prophet(prediction_start, prediction_end, dau_true['dau'], show_plot=False)
mape = mean_absolute_percentage_error(dau_true['dau'].reindex(pred.index), pred)
mapes.append(mape)
mapes = pd.DataFrame({'horizon': prediction_horizon, 'MAPE': mapes})
mapes

The MAPE error turns out to be high: 18% — 35%. The fact that the shortest horizon has the highest error means that the model is tuned for the long-term predictions. This is another inconvenience of such an approach: we have to tune the model for each prediction horizon. Anyway, this is our baseline. In the next section we’ll compare it with more advanced models.
4.2 General evaluation
In this section we evaluate the model implemented in the Section 3.6. So far we set the transition period as 1 year before the prediction start. We’ll study how the prediction depends on the transition period in the Section 4.3. As for the new users, we run the model using two options: the real values and the predicted ones. Similarly, we fix the same 3 prediction horizons and test the model on them.
The make_predicion helper function below implements the described options. It accepts prediction_start, prediction_end arguments defining the prediction period for a given horizon, new_users_mode which can be either true or predict, and transition_period. The options of the latter argument will be explained further.
import re
def make_prediction(prediction_start, prediction_end, new_users_mode='predict', transition_period='last_30d'):
prediction_start_minus_1d = pd.to_datetime(prediction_start) - pd.Timedelta('1d')
state0 = get_state0(prediction_start_minus_1d)
if new_users_mode == 'predict':
new_users_pred = predict_new_users(prediction_start, prediction_end, new_users, show_plot=False)
elif new_users_mode == 'true':
new_users_pred = new_users.copy()
if transition_period.startswith('last_'):
shift = int(re.search(r'last_(\d+)d', transition_period).group(1))
transitions_start = pd.to_datetime(prediction_start) - pd.Timedelta(shift, 'd')
M = get_transition_matrix(transitions, transitions_start, prediction_start_minus_1d)
dau_pred = predict_dau(M, state0, prediction_start, prediction_end, new_users_pred)
else:
transitions_start = pd.to_datetime(prediction_start) - pd.Timedelta(240, 'd')
M_base = get_transition_matrix(transitions, transitions_start, prediction_start_minus_1d)
dau_pred = pd.DataFrame()
month_starts = pd.date_range(prediction_start, prediction_end, freq='1MS')
N = len(month_starts)
for i, prediction_month_start in enumerate(month_starts):
prediction_month_end = pd.offsets.MonthEnd().rollforward(prediction_month_start)
transitions_month_start = prediction_month_start - pd.Timedelta('365D')
transitions_month_end = prediction_month_end - pd.Timedelta('365D')
M_seasonal = get_transition_matrix(transitions, transitions_month_start, transitions_month_end)
if transition_period == 'smoothing':
i = min(i, 12)
M = M_seasonal * i / (N - 1) + (1 - i / (N - 1)) * M_base
elif transition_period.startswith('seasonal_'):
seasonal_coef = float(re.search(r'seasonal_(0\.\d+)', transition_period).group(1))
M = seasonal_coef * M_seasonal + (1 - seasonal_coef) * M_base
dau_tmp = predict_dau(M, state0, prediction_month_start, prediction_month_end, new_users_pred)
dau_pred = pd.concat([dau_pred, dau_tmp])
state0 = dau_tmp.loc[prediction_month_end][states_order]
return dau_pred
def prediction_details(dau_true, dau_pred, show_plot=True, ax=None):
y_true = dau_true.reindex(dau_pred.index)['dau']
y_pred = dau_pred['dau']
mape = mean_absolute_percentage_error(y_true, y_pred)
if show_plot:
prediction_start = str(y_true.index.min().date())
prediction_end = str(y_true.index.max().date())
if ax is None:
y_true.plot(label='DAU true')
y_pred.plot(label='DAU pred')
plt.title(f'DAU prediction, {prediction_start} - {prediction_end}')
plt.legend()
else:
y_true.plot(label='DAU true', ax=ax)
y_pred.plot(label='DAU pred', ax=ax)
ax.set_title(f'DAU prediction, {prediction_start} - {prediction_end}')
ax.legend()
return mape
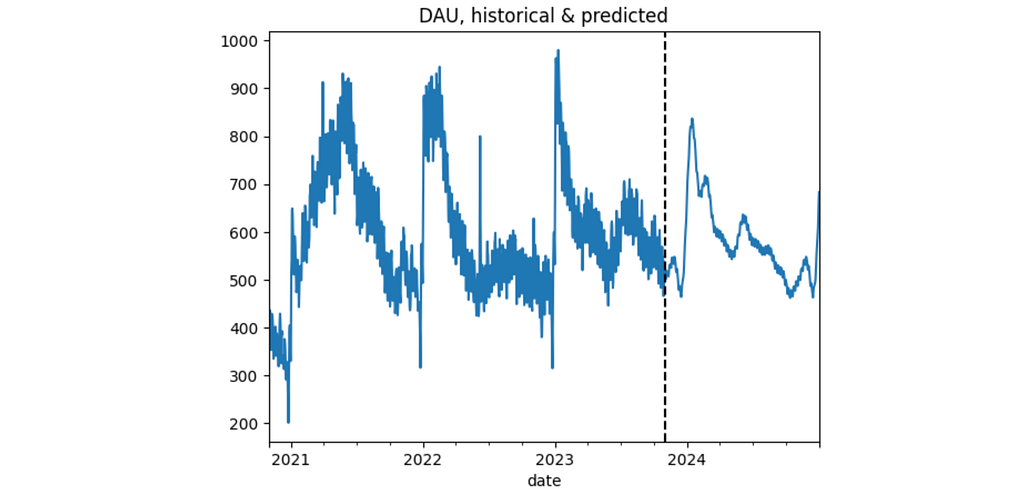
In total, we have 6 prediction scenarios: 2 options for new users and 3 prediction horizons. The diagram below illustrates the results. The charts on the left relate to the new_users_mode = 'predict' option, while the right ones relate to the new_users_mode = 'true' option.
fig, axs = plt.subplots(3, 2, figsize=(15, 6))
mapes = []
prediction_end = '2023-10-31'
prediction_horizon = [3, 6, 12]
for i, offset in enumerate(prediction_horizon):
prediction_start = pd.to_datetime(prediction_end) - pd.DateOffset(months=offset - 1)
prediction_start = prediction_start.replace(day=1)
args = {
'prediction_start': prediction_start,
'prediction_end': prediction_end,
'transition_period': 'last_365d'
}
for j, new_users_mode in enumerate(['predict', 'true']):
args['new_users_mode'] = new_users_mode
dau_pred = make_prediction(**args)
mape = prediction_details(dau_true, dau_pred, ax=axs[i, j])
mapes.append([offset, new_users_mode, mape])
mapes = pd.DataFrame(mapes, columns=['horizon', 'new_users', 'MAPE'])
plt.tight_layout()
And here are the MAPE values summarizing the prediction quality:
mapes.pivot(index='horizon', columns='new_users', values='MAPE')

We notice multiple things.
- In general, the model demonstrates much better results than the baseline. Indeed, the baseline is based on the historical DAU data only, while the model uses the user states information.
- However, for the 1-year horizon and new_users_mode='predict' the MAPE error is huge: 65%. This is 3 times higher than the corresponding baseline error (21%). On the other hand, new_users_mode='true' option gives a much better result: 8%. It means that the new users prediction has a huge impact on the model, especially for long-term predictions. For the shorter periods the difference is less dramatic. The major reason for such a difference is that 1-year period includes Christmas with its extreme values. As a result, i) it's hard to predict such high new user values, ii) the period heavily impacts user behavior, the transition matrix and, consequently, DAU values. Hence, we strongly recommend to implement the new user prediction carefully. The baseline model was specially tuned for this Christmas period, so it's not surprising that it outperforms the Markov model.
- When the new users prediction is accurate, the model captures trends well. It means that using last 365 days for the transition matrix calculation is a reasonable choice.
- Interestingly, the true new users data provides worse results for the 3-months prediction. This is nothing but a coincidence. The wrong new users prediction in October 2023 reversed the predicted DAU trend and made MAPE a bit lower.
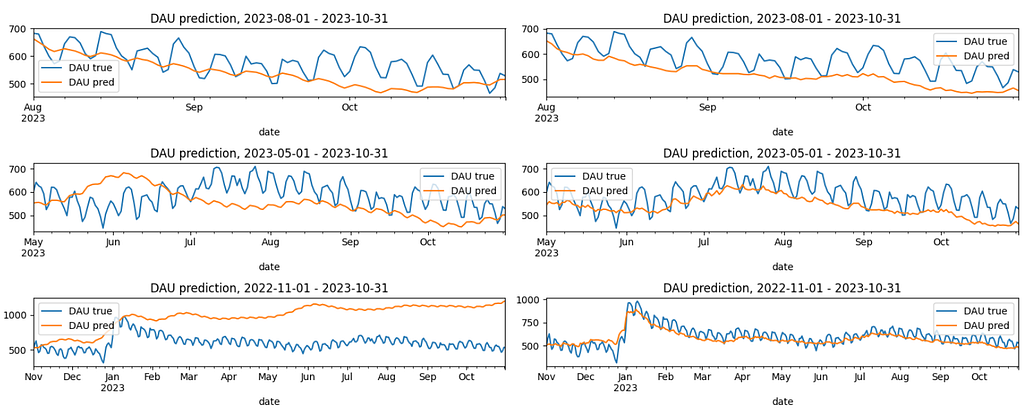
Now, let’s decompose the prediction error and see which states contribure the most. By error we mean here dau_pred - dau_true values, by relative error - ( dau_pred - dau_true) / dau_true - see left and right diagrams below correspondingly. In order to focus on this aspect, we'll narrow the configuration to the 3-months prediction horizon and the new_users_mode='true' option.
dau_component_cols = ['new', 'current', 'reactivated', 'resurrected']
dau_pred = make_prediction('2023-08-01', '2023-10-31', new_users_mode='true', transition_period='last_365d')
figure, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
dau_pred[dau_component_cols]\
.subtract(dau_true[dau_component_cols])\
.reindex(dau_pred.index)\
.plot(title='Prediction error by state', ax=ax1)
dau_pred[['current']]\
.subtract(dau_true[['current']])\
.div(dau_true[['current']])\
.reindex(dau_pred.index)\
.plot(title='Relative prediction error (current state)', ax=ax2);
From the left chart we notice that the error is basically contributed by the current state. It's not surprising since this state contributes to DAU the most. The error for the reactivated, and resurrected states is quite low. Another interesting thing is that this error is mostly negative for the current state and mostly positive for the resurrected state. The former might be explained by the fact that the new users who appeared in the prediction period are more engaged that the users from the past. The latter indicates that the resurrected users in reality contribute to DAU less than the transition matrix expects, so the dormant→ resurrected conversion rate is overestimated.
As for the relative error, it makes sense to analyze it for the current state only. This is because the daily amount of the reactivated and resurrected states are low so the relative error is high and noisy. The relative error for the current state varies between -25% and 4% which is quite high. And since we've fixed the new users prediction, this error is explained by the transition matrix inaccuracy only. In particular, the current→ current conversion rate is roughly 0.8 which is high and, as a result, it contributes to the error a lot. So if we want to improve the prediction we need to consider tuning this conversion rate foremost.
4.3 Transitions period impact
In the previous section we kept the transitions period fixed: 1 year before a prediction start. Now we’re going to study how long this period should be to get more accurate prediction. We consider the same prediction horizons of 3, 6, and 12 months. In order to mitigate the noise from the new users prediction, we use the real values of the new users amount: new_users_mode='true'.
Here comes varying of the transition_period argument. Its values are masked with the last_ It turns out that the optimal transitions period depends on the prediction horizon. Shorter horizons require shorter transitions periods: the minimal MAPE error is achieved at 1, 4, and 8 transition periods for the 3, 6, and 12 months correspondingly. Apparently, this is because the longer horizons contain some seasonal effects that could be captured only by the longer transitions periods. Also, it seems that for the longer prediction horizons the MAPE curve is U-shaped meaning that too long and too short transitions periods are both not good for the prediction. We’ll develop this idea in the next section. Nevertheless, fixing a single transition matrix for predicting the whole year ahead doesn’t seem to be a good idea: such a model would be too rigid. Usually, user behavior varies depending on a season. For example, users who appear after Christmas might have some shifts in behavior. Another typical situation is when users change their behavior in summer. In this section, we’ll try to take into account these seasonal effects. So we want to predict DAU for 1 year ahead starting from November 2022. Instead of using a single transition matrix M_base which is calculated for the last 8 months before the prediction start, according to the previous subsection results (and labeled as the last_240d option below), we'll consider a mixture of this matrix and a seasonal one M_seasonal. The latter is calculated on monthly basis lagging 1 year behind. For example, to predict DAU for November 2022 we define M_seasonal as the transition matrix for November 2021. Then we shift the prediction horizon to December 2022 and calculate M_seasonal for December 2021, etc. In order to mix M_base and M_seasonal we define the following two options. According to the MAPE errors, seasonal_0.3 configuration provides the best results. Interestingly, smoothing approach has appeared to be even worse than the last_240d. From the diagram above we see that all three models start to underestimate the DAU values in July 2023, especially the smoothing model. It seems that the new users who started appearing in July 2023 are more engaged than the users from 2022. Probably, the app was improved sufficiently or the marketing team did a great job. As a result, the smoothing model that much relies on the outdated transitions data from July 2022 - October 2022 fails more than the other models. To sum things up, let’s make a final prediction for the 2024 year. We use the seasonal_0.3 configuration and the predicted values for new users. In the Section 4 we studied the model performance from the prediction accuracy perspective. Now let’s discuss the model from the practical point of view. Besides poor accuracy, predicting DAU as a time-series (see the Section 4.1) makes this approach very stiff. Essentially, it makes a prediction in such a manner so it would fit historical data best. In practice, when making plans for a next year we usually have some certain expectations about the future. For example, Our model can take into account such expectations. For the examples above we can adjust the new users prediction, the new→ current and the current→ current conversion rates respectively. As a result, we can get a prediction that doesn't match with the historical data but nevertheless would be more realistic. This model's property is not just flexible - it's interpretable. You can easily discuss all these adjustments with the stakeholders, and they can understand how the prediction works. Another advantage of the model is that it doesn’t require predicting whether a certain user will be active on a certain day. Sometimes binary classifiers are used for this purpose. The downside of this approach is that we need to apply such a classifier to each user including all the dormant users and each day from a prediction horizon. This is a tremedous computational cost. In contrast, the Markov model requires only the initial amount of states ( state0). Moreover, such classiffiers are often black-box models: they are poorly interpretable and hard to adjust. The Markov model also has some limitations. As we already have seen, it’s sensitive to the new users prediction. It’s easy to totally ruin the prediction by a wrong new users amount. Another problem is that the Markov model is memoryless meaning that it doesn’t take into account the user’s history. For example, it doesn’t distinguish whether a current user is a newbie, experienced, or reactivated/ resurrected one. The retention rate of these user types should be certainly different. Also, as we discussed earlier, the user behavior might be of different nature depending on the season, marketing sources, countries, etc. So far our model is not able to capture these differences. However, this might be a subject for further research: we could extend the model by fitting more transition matrices for different user segments. Finally, as we promised in the introduction, we provide a DAU spreadsheet calculator. In the Prediction sheet you'll need to fill the initial states distribution row (marked with blue) and the new users prediction column (marked with purple). In the Conversions sheet you can adjust the transition matrix values. Remember that the sum of each row of the matrix should be equal to 1. That’s all for now. I hope that this article was useful for you. In case of any questions or suggestions, feel free to ask in the comments below or contact me directly on LinkedIn. All the images in the post are generated by the author. Modeling DAU with Markov Chain was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story. result = []
for prediction_offset in prediction_horizon:
prediction_start = pd.to_datetime(prediction_end) - pd.DateOffset(months=prediction_offset - 1)
prediction_start = prediction_start.replace(day=1)
for transition_offset in range(1, 13):
dau_pred = make_prediction(
prediction_start, prediction_end, new_users_mode='true',
transition_period=f'last_{transition_offset*30}d'
)
mape = prediction_details(dau_true, dau_pred, show_plot=False)
result.append([prediction_offset, transition_offset, mape])
result = pd.DataFrame(result, columns=['prediction_period', 'transition_period', 'mape'])
result.pivot(index='transition_period', columns='prediction_period', values='mape')\
.plot(title='MAPE by prediction and transition period');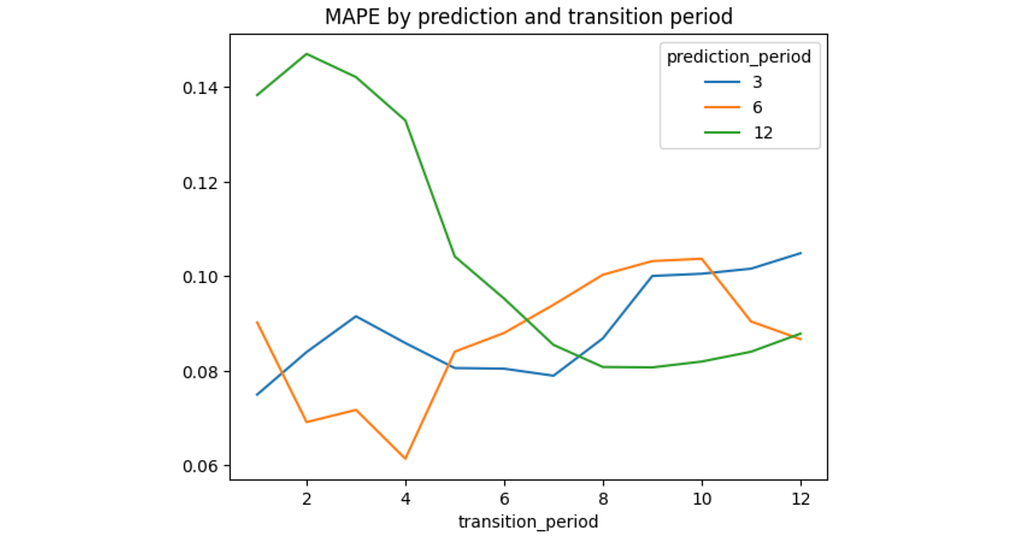
4.4 Obsolence and seasonality
result = pd.DataFrame()
for transition_period in ['last_240d', 'seasonal_0.3', 'smoothing']:
result[transition_period] = make_prediction(
'2022-11-01', '2023-10-31',
'true',
transition_period
)['dau']
result['true'] = dau_true['dau']
result['true'] = result['true'].astype(int)
result.plot(title='DAU prediction by different transition matrices');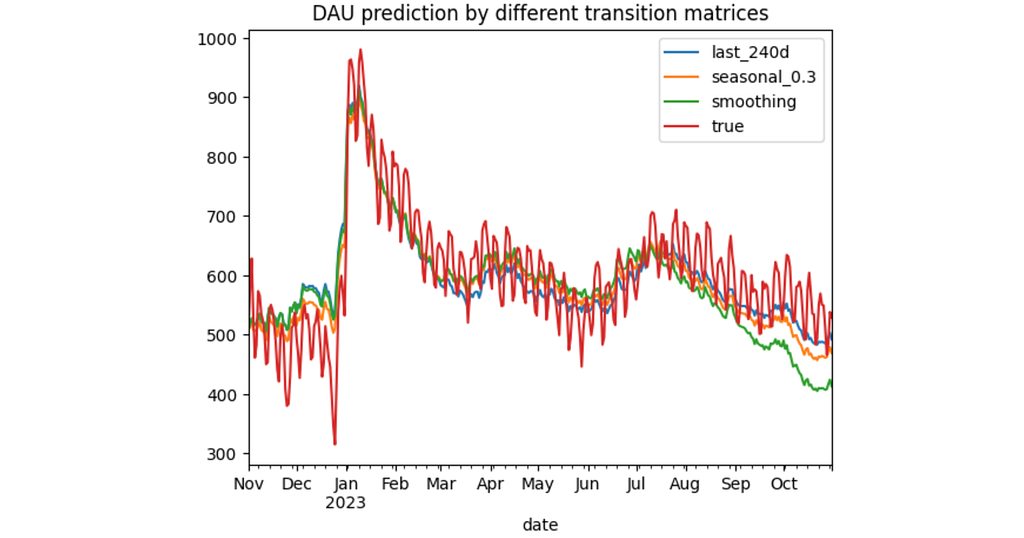
mape = pd.DataFrame()
for col in result.columns:
if col != 'true':
mape.loc[col, 'mape'] = mean_absolute_percentage_error(result['true'], result[col])
mape
4.5 Final solution
dau_pred = make_prediction(
PREDICTION_START, PREDICTION_END,
new_users_mode='predict',
transition_period='seasonal_0.3'
)
dau_true['dau'].plot(label='true')
dau_pred['dau'].plot(label='seasonal_0.3')
plt.title('DAU, historical & predicted')
plt.axvline(PREDICTION_START, color='k', linestyle='--')
plt.legend();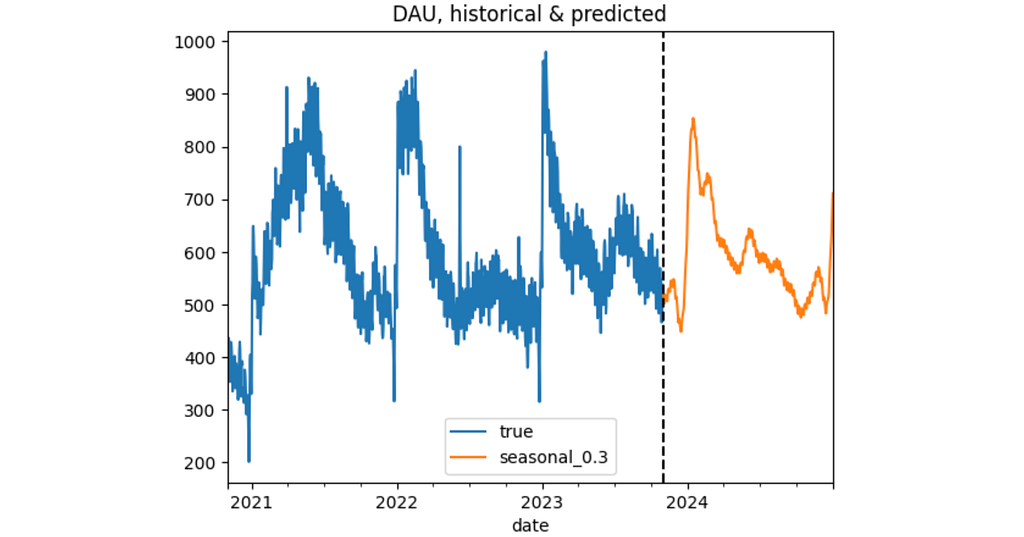
5. Discussion


 Editor-Admin
Editor-Admin 





